Kriging con Deriva Externa: Guia Completa.
¡Bienvenidos al intrigante mundo del Kriging con Deriva Externa! ¿Conoces el uso extendido de esta técnica de interpolación espacial? Esta técnica se emplea en diversas disciplinas, incluyendo la mineralogía, hidrogeología, geología y climatología, entre otras ciencias de la Tierra. Si te interesa aprender más sobre cómo aplicar esta potente técnica en tus análisis geoespaciales, has llegado al lugar correcto.
En esta guía definitiva, creada por la Comunidad GeoRGB y disponible en https://giscourse.online, te presentamos los pasos esenciales para realizar con éxito el Kriging con Deriva Externa. Siguiendo cuidadosamente estos pasos, estarás en el camino correcto para obtener resultados precisos y confiables en tus proyectos mediambientales.
Además, descubrirás cómo esta técnica te ayudará a comprender mejor los datos espaciales y a tomar decisiones informadas en tus investigaciones. Entonces, ¿qué esperas? ¡Únete a nosotros en este emocionante viaje y aprendamos juntos!
¿Qué es el kriging con Deriva Externa?
El Kriging con Deriva Externa (KED, por sus siglas en inglés, Kriging with External Drift) es un método utilizado en la interpolación espacial. Este enfoque se aplica cuando contamos con una variable secundaria, también conocida como variable externa, que muestra una correlación con la variable principal que estamos estudiando. Dicha correlación se utiliza para potenciar la precisión de nuestras estimaciones.
El concepto subyacente en el Kriging con Deriva Externa es que la variable principal puede ser modelada como una función determinista (la “deriva”) más un componente estocástico (o aleatorio). Para modelar la deriva, se emplea la variable secundaria. Así, la variable principal Z en un punto en el espacio, “s”, se puede expresar como la suma de una función determinista μ(s) y un término estocástico ε(s).
Z(s)= μ(s)+ε(s)
Por ejemplo, supongamos que deseas predecir la concentración de un contaminante en un río (variable primaria). Si sabes que esta concentración está correlacionada con la temperatura del agua (variable externa), puedes usar Kriging con Deriva Externa. Esta técnica te ayudará a mejorar la precisión de las predicciones.
El Kriging con Deriva Externa es especialmente útil cuando se tiene valores de la variable secundaria en toda la grilla de interpolación, pero solo unos pocas muestras de la variable primaria en el area de estudio. En estos casos, el Kriging con Deriva Externa puede proporcionar estimaciones más precisas que el kriging ordinario.
El Kriging con Deriva Externa es similar al Kriging Universal, sin embargo, hay una distinción importante entre ambos. El Kriging Universal usa coordenadas geográficas para determinar la tendencia en los datos. En cambio, el Kriging con Deriva Externa usa una variable externa para establecerla.
Preparación de datos para Kriging con Deriva Externa
Paso 1: Recopilación de datos
La recopilación de datos es el primer paso para cualquier análisis geoespacial. Aquí te dejo una serie de aspectos a considerar durante este proceso:
a. Ubicación de las muestras: Debes tener datos de las ubicaciones (generalmente en coordenadas geográficas o en un sistema de coordenadas proyectado, UTM es la mejor opcion en la mayoria de los casos) donde se han tomado las muestras o mediciones. Estos datos son fundamentales para el análisis espacial y para el Kriging con deriva externa.
b. Variable de interés: Necesitas datos de la variable que deseas interpolar. Pueden ser mediciones de cualquier tipo, como concentraciones de minerales, valores de precipitación, profundidad del nivel freático, etc.
c. Variables de deriva (externa): Estas son variables adicionales que crees que pueden explicar la variación en tu variable de interés. Las variables externas suelen obtenerse de fuentes de sensores remotos, incluyendo, pero no limitándose a, imágenes satelitales, LiDAR, radares, y Modelos Digitales de Elevación (MDE). Alternativamente, estas variables también pueden ser calculadas en un entorno de oficina, basándose en elementos identificables en imágenes del terreno, mapas topográficos, morfológicos y similares. Estos recursos facilitan la computación de distancias relevantes, como la proximidad a la costa o a un río, entre otros.
Es esencial comprender que la variable externa debe estar presente en cada píxel de la malla de interpolación, así como también en la misma ubicación de la muestra o lugar de medición. Este aspecto es crucial para el correcto funcionamiento del método de interpolación. Más adelante, en este tutorial, veremos cómo manejar la malla de interpolación.
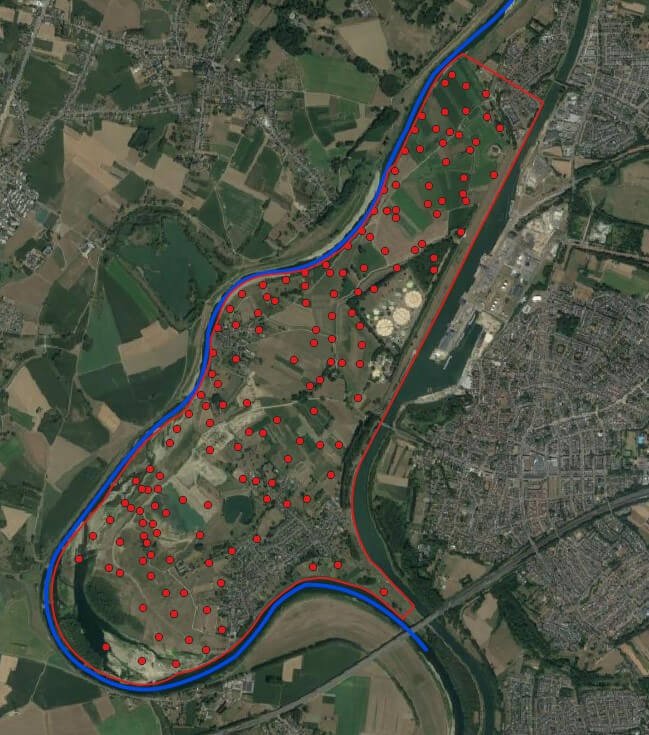
Distribución espacial de los datos asociados con la concentración de zinc en el área de estudio delimitada. Esta zona, queda bordeada por el rio Meuse.
Paso 2: Verificación de los datos
La verificación de los datos es un paso esencial en cualquier análisis para garantizar la precisión y la confiabilidad de tus resultados. Aquí están algunos de los puntos clave a considerar:
a. Verificación de la coherencia: Revisa tus datos para asegurarte de que no hay valores incoherentes o fuera de lo esperado. Por ejemplo, si estás trabajando con datos de temperatura, un valor de -273 grados Celsius sería incoherente en la mayoría de los contextos.
b. Consistencia de las unidades: Asegúrate de que todas tus medidas estén en las mismas unidades. Por ejemplo, si estás trabajando con datos de distancia, es posible que tengas algunas medidas en kilómetros y otras en millas. Deberás convertir todas las medidas a la misma unidad para que puedan ser comparadas de manera efectiva.
c. Correspondencia de ubicaciones y mediciones: Verifica que las mediciones correspondan a las ubicaciones correctas. Por ejemplo, si tienes un conjunto de datos de mediciones de temperatura y un conjunto de datos de ubicaciones geográficas, debes asegurarte de que cada medición de temperatura se corresponda con la ubicación geográfica correcta.
d. Verificación de duplicados: Los datos duplicados pueden distorsionar tus resultados, por lo que debes verificar si hay observaciones duplicadas en tu conjunto de datos y decidir cómo manejarlas.
e. Análisis de outliers: Estos son valores notablemente distintos en tus datos, originados por errores o observaciones reales. Su presencia afecta significativamente los resultados.
Recuerda que la verificación de datos es un proceso continuo que deberías realizar a lo largo de todo tu análisis.
Paso 3: Análisis exploratorio de datos
En el contexto de Kriging con Deriva Externa (KED), el análisis exploratorio de datos implica varios pasos clave que te ayudarán a entender la estructura y las propiedades de tus datos:
a. Visualización espacial: Dado que estás trabajando con datos geoespaciales, uno de los primeros pasos debe ser visualizar tus datos en el espacio. Esto puede implicar la creación de mapas de dispersión de tus datos para ver dónde se encuentran tus puntos de muestreo y cómo se distribuyen los valores de tu variable de interés y de la variable externa en el espacio. Esta visualización te ayudará a identificar cualquier patrón espacial o áreas de interés.
b. Análisis de distribución: Es útil entender la distribución de tu variable de interés y de la variable externa. Esto podría implicar la creación de histogramas, gráficos de caja y bigotes (boxplots), y la realización de pruebas de normalidad.
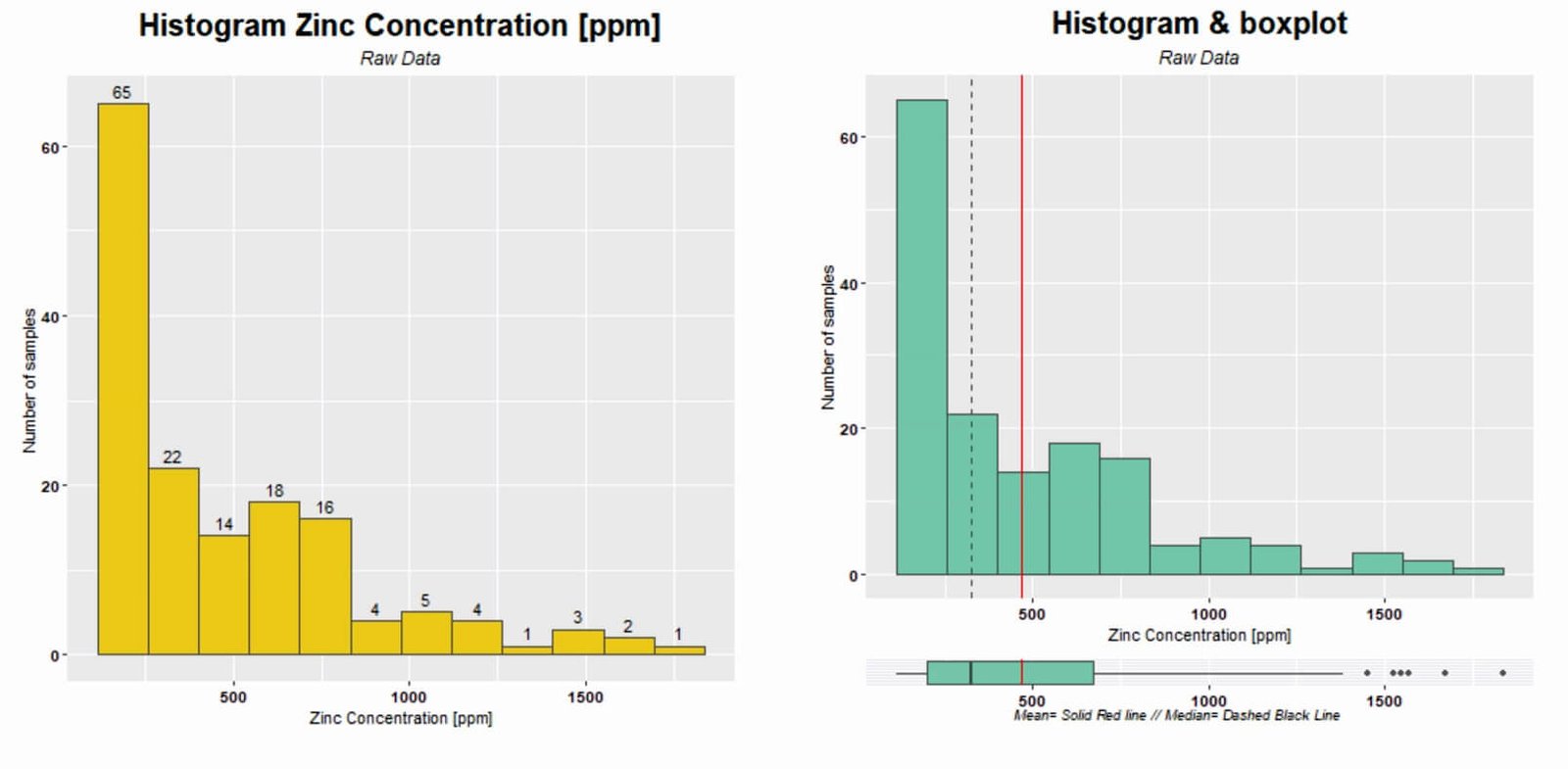
Izquierda: histograma con el numero de mustras encima de cada contenedor. Derecha: Histograma y diagrama de caja juntos, con la media y la mediana.
c. Transformación de datos y Normalidad: En muchos métodos de análisis estadístico y geostadístico, incluyendo el Kriging con Deriva Externa, se asume que los datos siguen una distribución normal. Sin embargo, en la práctica, esto no siempre es cierto. Para garantizar la normalidad en Kriging con Deriva Externa, primero verifica la normalidad de tus datos mediante histogramas, gráficos Q-Q o pruebas estadísticas. Si no son normales, aplica transformaciones, como la logarítmica, raíz cuadrada o Box-Cox, entre otras. Tras transformar, revisa nuevamente la normalidad. Finalmente, usa los datos transformados en el KED, recordando que podrías necesitar revertir la transformación para la interpretación y creación de mapas finales.
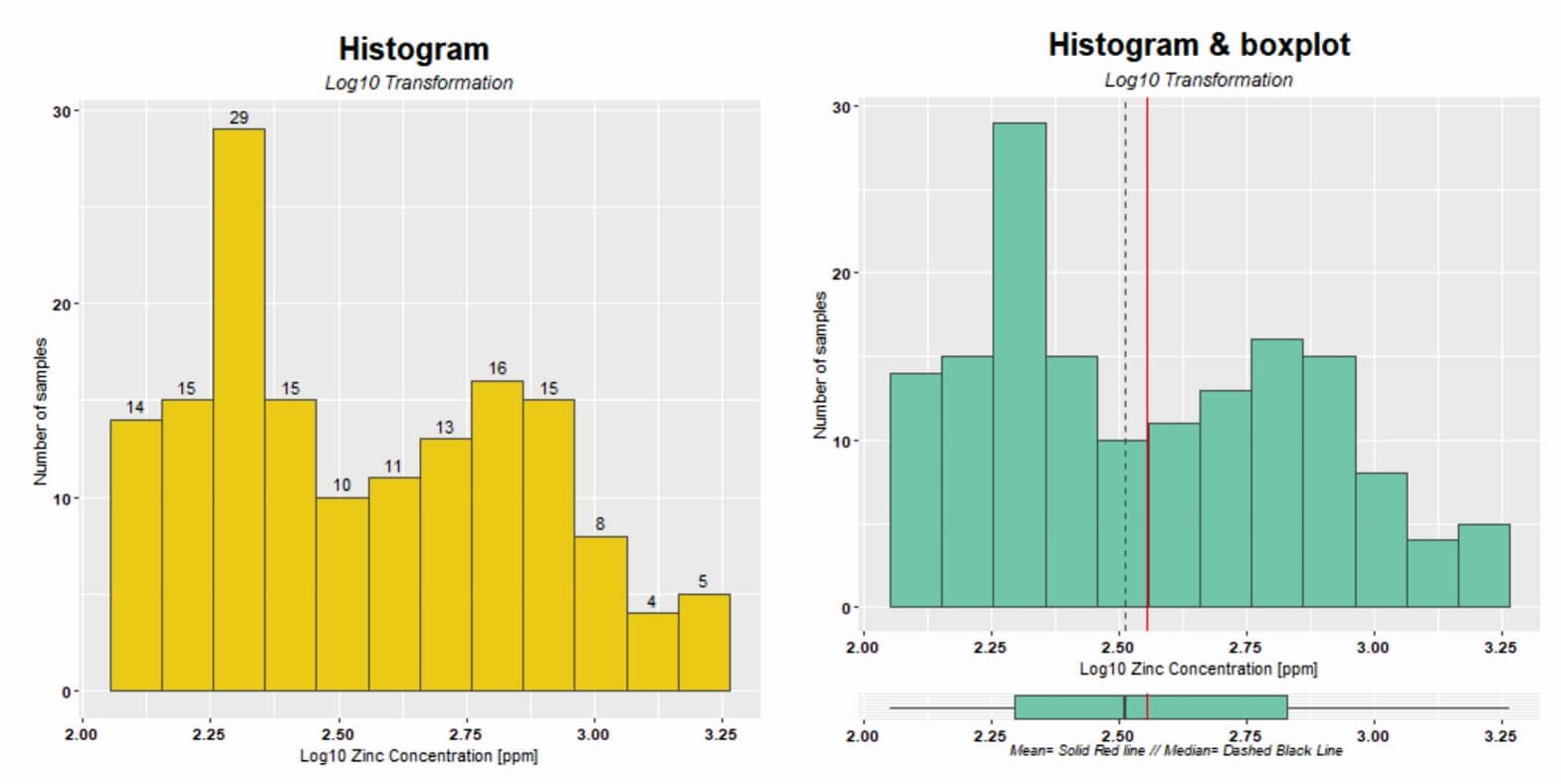
Izquierda: histograma con los datos transformados, mostrando el numero de mustras encima de cada contenedor. Derecha: Histograma y diagrama de caja juntos de los datos transformados, con la media y la mediana.
d. Análisis de tendencias: El Kriging con Deriva Externa (KED) opera bajo la premisa de que existe una función de deriva que influye en la variación de la variable principal. Por lo tanto, es crucial realizar un análisis de tendencias para discernir cualquier patrón latente en tus datos, lo que podría incluir la creación de gráficos de tendencia. Adicionalmente, debido a que se emplea una variable externa para ayudar a explicar parte de la variación en la variable principal, es fundamental entender la interrelación entre ambas. Para ello, puedes generar gráficos de dispersión y llevar a cabo análisis de correlación, mientras que la aplicación de análisis de regresión puede reservarse para la exploración detallada de la función de deriva. El hecho de que la variable principal y la variable externa se encuentren en la misma ubicación facilita enormemente este tipo de análisis.
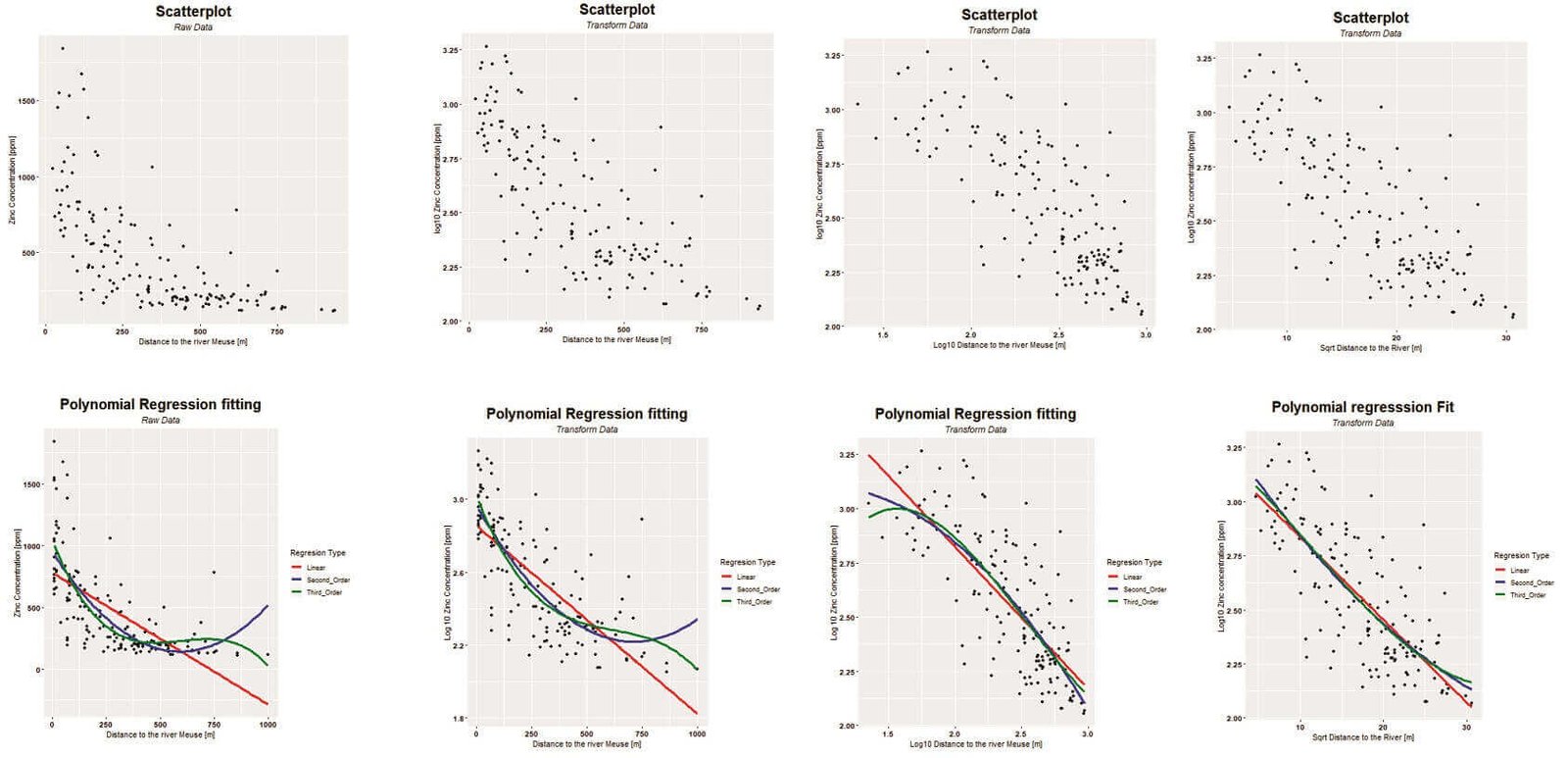
En la parte superior se muestran gráficos de dispersión. Estos ilustran la relación entre la variable principal y la externa, con datos tanto transformados como originales. En la sección inferior se muestran gráficos de dispersión en los cuales se han ajustado modelos polinómicos de tendencia. El objetivo es identificar el modelo que mejor se ajusta a los datos. Esto se determina en función de su respectiva transformación.
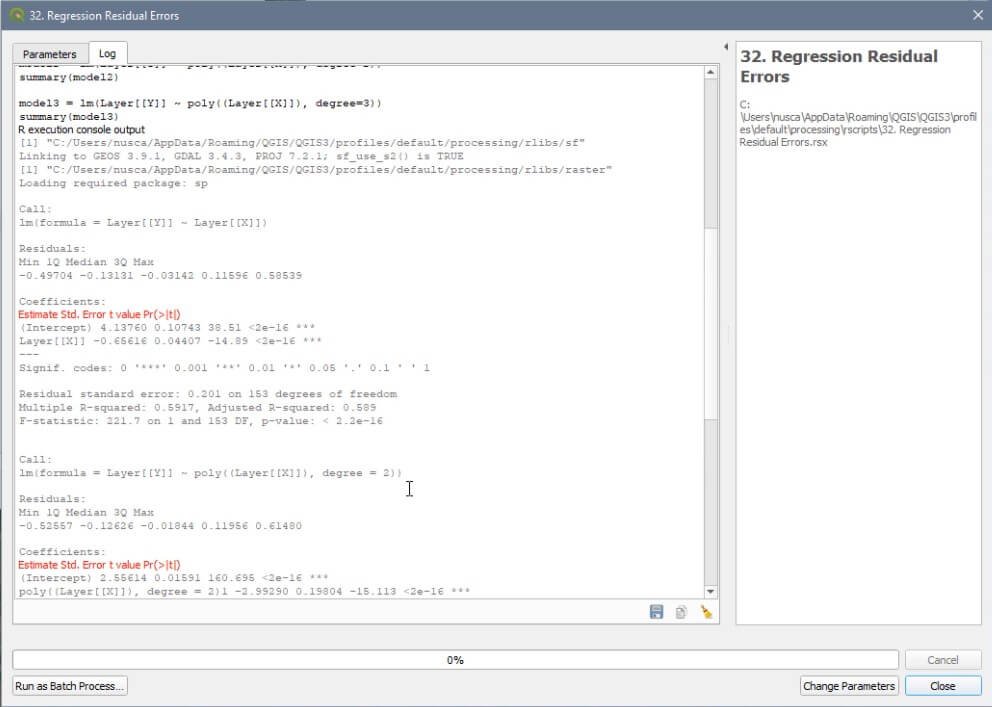
Analysis de regresión ejecutado con la interfaz de QGIS.
e. Análisis de variogramas: El análisis variográfico es una herramienta importante para entender la estructura de los datos espaciales. A través de él, se pueden obtener diferentes parámetros como el rango, la autocorrelación espacial, el efecto nugget y la meseta parcial. Estos parámetros son relevantes para la modelización y predicción de valores espaciales, ya que permiten entender la variabilidad de los datos y cómo se relacionan espacialmente. El efecto nugget, por ejemplo, representa la variabilidad no explicada por la estructura espacial del variograma, mientras que la meseta parcial indica la cantidad de variabilidad que se puede explicar mediante la estructura espacial. Si la meseta parcial es alta, significa que hay una estructura espacial clara en los datos, lo que facilita la modelización del variograma y la realización del Kriging con deriva externa.
Una vez creado el variograma, se procede a seleccionar el modelo que mejor se ajuste a los datos. El modelo del variograma es una función matemática que describe la estructura de correlación espacial de los datos. Esta estructura queda perfectamente cuantificada con los valores del rango, la meseta parcial y el efecto nugget.
La selección del modelo del variograma adecuado es crucial para obtener resultados precisos en el Kriging con deriva externa. Existen varios modelos de variograma disponibles, cada uno con sus propias ventajas y desventajas. Algunos de los modelos de variograma más comunes incluyen el modelo esférico, el modelo exponencial y el modelo gaussiano.
La selección del modelo del variograma no es una tarea fácil. Esta selección se basa en la distribución de los datos del variograma y en la elección de un modelo adecuado. Por lo tanto, se requiere un análisis cuidadoso para lograr una buena selección del modelo del variograma. Al final, es recomendable probar varios modelos de variograma para determinar el más adecuado a los datos disponibles.
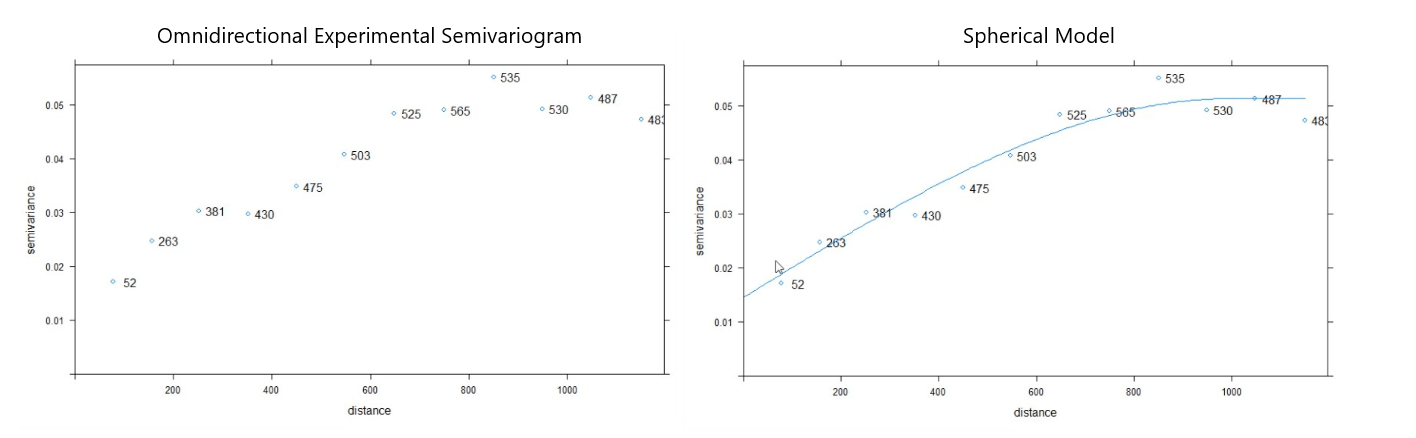
Análisis del variograma y ajuste del modelo esférico, implementación con RStudio.
Paso 4: Creación de la malla de interpolación
La creación de la malla de interpolación es un paso crucial en el proceso de Kriging con Deriva Externa (KED). La malla de interpolación es una red de puntos en el espacio geográfico. Para estos puntos, estimas valores usando tus datos existentes. Aquí te detallo los pasos básicos para su creación:
a. Definir la extensión geográfica: El primer paso para crear una malla de interpolación es definir la extensión geográfica de tu área de estudio. Esta extensión debe cubrir todas las ubicaciones para las que quieres hacer estimaciones.
b. Definir la resolución de la malla: La resolución de la malla se refiere al tamaño de cada celda o pixel en la malla. Cuanto más pequeño sea el tamaño de la celda, mayor será la resolución de tu malla y más detallada será tu interpolación. Sin embargo, una mayor resolución también requiere más tiempo de cálculo y más espacio de almacenamiento. Por lo general, la resolución de la malla viene dada por la distancia mínima entre las muestras de la variable principal, sin embargo, en este caso, también puede estar condicionada por las dimensiones del píxel del raster de la variable externa.
c. Generar la malla: Una vez que hayas definido la extensión y la resolución, puedes generar la malla. Esto implica crear una matriz de puntos que cubra toda tu extensión geográfica con la resolución especificada.
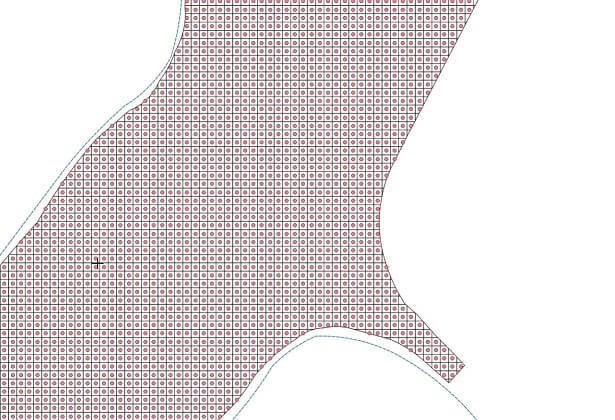
Matriz de puntos asociada a la malla de interpolación.
d. Asignar los valores de la variable externa a la malla: Esta es una parte crítica y fundamental en el KED, que la hace completamente diferente a cualquier otro tipo de malla de interpolación En KED necesitas asignar un valor de tu variable externa a cada punto en tu malla de interpolación. Esto se puede hacer utilizando datos de sensores remotos, modelos digitales de elevación, mapas topográficos, u otras fuentes de datos geoespaciales.
Por último, es importante tener en cuenta que la malla de interpolación debe ser representativa de la distribución espacial de los datos. Si tu malla no cubre adecuadamente las ubicaciones de tus datos, tus estimaciones podrían ser sesgadas o imprecisas.

Cálculo de la variable externa en la matriz de puntos. En este caso, la variable externa es la distancia mínima al río.
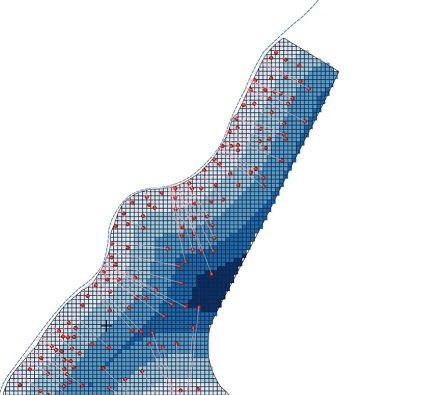
Se muestra un raster final que indica la distancia al río. También se representa la distancia al río con puntos rojos desde el conjunto de datos.
Paso 5: Interpolación usando Kriging con Deriva Externa
En última instancia, la estimación por KED es la suma del modelo estocástico y del modelo determinista. El KED combina estos dos modelos de manera totalmente automática. Esta combinación es posible gracias a la información proporcionada durante los pasos anteriores, como la selección de la variable externa y el modelo de semivariograma. El resultado de la interpolación se puede utilizar para generar mapas de contorno y superficies de distribución de los datos. Esta información puede ser útil para la toma de decisiones en proyectos ambientales y otros campos relacionados.
La precisión de la interpolación depende de la calidad de los datos utilizados. Además, es crucial la elección de la variable externa y el modelo de semivariograma. Por lo tanto, es crucial considerar ambos factores para obtener una interpolación precisa. Es necesario realizar una validación cruzada para garantizar resultados fiables. Además, otros mecanismos de evaluación también deben emplearse.
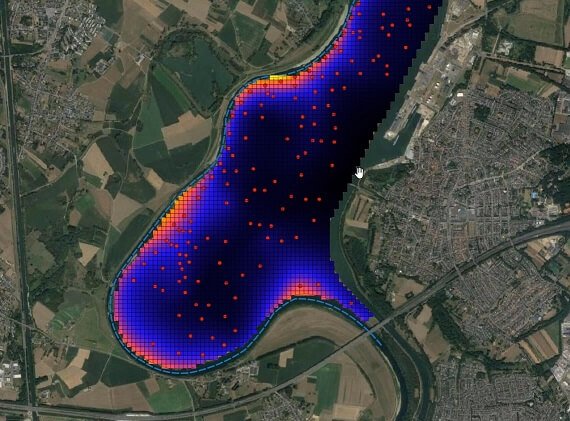
Resultado final de la interpolación.
Paso 6: Validación cruzada para KED
La validación cruzada es una técnica comúnmente utilizada en estadística para evaluar la capacidad de generalización de un modelo. En el contexto del KED, esta técnica puede ser utilizada para validar la precisión y robustez de la interpolación.
Aquí, presento un esquema básico para implementar la validación cruzada K-Fold en KED. Sin embargo, es relevante mencionar otras técnicas. Un ejemplo popular es la validación cruzada dejando uno fuera, (o LOOCV por sus siglas en inglés):
- Dividir el conjunto de datos en subconjuntos (típicamente, se utilizan 5 o 10). Estos subconjuntos deben ser representativos del conjunto de datos original.
- Para cada subconjunto, ajusta el modelo KED utilizando los datos restantes. Es decir, todos los datos excepto los del subconjunto actual.
- Usa el modelo ajustado para predecir los valores en el subconjunto actual. Estos datos no se utilizaron para ajustar el modelo.
- Comparar las predicciones con los valores reales y registrar alguna medida de error (por ejemplo, el error cuadrático medio).
- Repetir los pasos 2-4 para cada subconjunto.
- Calcular un promedio de las medidas de error registradas. Esto proporcionará una estimación de cómo de bien el modelo KED se comportará con datos nuevos.
Recuerda que, en general, es deseable contar con un número adecuado de muestras para realizar una validación sólida. Si el tamaño de la muestra es muy pequeño, la incertidumbre en la estimación puede ser alta. En tal caso, es crucial considerar otras fuentes de información. Datos auxiliares o conocimientos de un experto en el area pueden mejorar la calidad de las predicciones.
Ejemplo práctico con QGIS y R, basado en kriging con Deriva Externa
Nos complace presentarte un fascinante tutorial en dos partes que despliega un ejercicio práctico de kriging con deriva externa. Este tutorial te guiará en el proceso detallado de interpolación, paso a paso. El enfoque será estimar la concentración de zinc para la identificación de suelos contaminados.
A través de este instructivo, el mentor te guiará en cada etapa del proceso de interpolación. Cubre desde la entrada y exploración de datos hasta la aplicación del KED. El tutorial culmina con la interpretación detallada de los resultados, permitiéndote absorber el máximo valor de cada paso del ejercicio.
Este tutorial está diseñado para ser intuitivo y accesible. No en vano, está orientado a personas con conocimientos básicos de GIS y R. Las explicaciones claras y las ilustraciones visuales facilitan la comprensión de todos los conceptos.
Al concluir este tutorial, habrás adquirido valiosa experiencia práctica en el uso del kriging con deriva externa. Además, estarás equipado con las habilidades necesarias para aplicar este método en tus propios proyectos. Los conocimientos adquiridos aquí se pueden aplicar en diversos campos. Entre ellos se encuentran la geología y las ciencias ambientales.
Nuestro objetivo final es que adquieras competencias sólidas en el análisis de datos espaciales, utilizando una variedad de herramientas. Así, podrás enfrentarte a desafíos reales y hacer contribuciones significativas en tu campo de estudio o trabajo. ¡Estás a solo un clic de iniciar esta emocionante travesía en el mundo del kriging con deriva externa!
Cuarta lección del cuarto curso de Geoestadística: Interpolación y mapeo de kriging/cokriging, impartido en https://giscourse.online/
Conviértete en un experto en geoestadística hoy mismo
Si estás buscando expandir tus habilidades en análisis geostadístico, ¡este curso es para ti!. Este Curso de Geostadística sobre Interpolación y Mapeo Kriging/Cokriging te brindará una comprensión profunda de los diferentes tipos de Kriging. Lo cual, te facilitara el análisis de datos espaciales y la creación de mapas totalmente profesionales. El curso presenta ejemplos reales y ejercicios prácticos utilizando R integrado en QGIS. No cabe duda, que es la elección perfecta para aquellos que deseen llevar su análisis geoestadístico al siguiente nivel. No esperes más, ¡accede ahora y comienza a aprender hoy!.

5 Ventajas del kriging con Deriva Externa
El Kriging con Deriva Externa (KED) es un método geostadístico flexible y poderoso para la interpolación de datos espaciales. A continuación, te muestro cinco ventajas clave de utilizar KED:
a. Incorporación de información adicional: A diferencia del Kriging ordinario, el KED permite la incorporación de información adicional en forma de una variable externa. Esto puede ayudar a mejorar la precisión de la interpolación, especialmente cuando la variable externa está fuertemente correlacionada con la variable de interés.
b. Manejo de tendencias espaciales: El KED puede manejar eficazmente tendencias espaciales en los datos, lo cual es especialmente útil en situaciones donde los datos muestran un cambio sistemático en una dirección particular. Esto se hace a través de la función de deriva que se incluye en el modelo.
c. Estimación de la incertidumbre: Al igual que otros métodos de Kriging, el KED proporciona no solo una estimación de los valores en ubicaciones no muestreadas, sino también una medida de la incertidumbre asociada a esas estimaciones. Esto puede ser invaluable para la toma de decisiones basada en riesgo.
d. Interpolación optimizada: El KED, al igual que otros métodos de Kriging, utiliza la teoría de la estimación óptima. Esto significa que, bajo ciertas suposiciones, las estimaciones de KED son, en un sentido estadístico, las mejores posibles.
e. Flexibilidad: El KED es flexible en términos de la forma de la función de deriva que se puede utilizar. Esta puede ser una función lineal de las coordenadas espaciales, una función de las variables externas, o una combinación de ambas. Esto permite adaptar el modelo a la estructura particular de tus datos.
5 Desventajas del kriging con Deriva Externa:
El Kriging con Deriva Externa (KED) tiene muchas ventajas. Sin embargo, es importante considerar sus limitaciones al utilizar este método. Aquí se enumeran cinco de ellas:
a. Suposiciones estadísticas: El KED, al igual que otros métodos de Kriging, hace ciertas suposiciones sobre los datos, incluyendo la estacionariedad y la normalidad. Si estas suposiciones no se cumplen, las estimaciones de KED pueden ser sesgadas o inexactas.
b. Selección de la variable externa: La elección de la variable externa en el KED puede ser desafiante. Si la variable externa no está bien correlacionada con la variable de interés, su inclusión puede no mejorar, e incluso podría deteriorar, la precisión de la interpolación.
c. Complejidad computacional: El KED puede ser computacionalmente intensivo, especialmente para conjuntos de datos grandes y para mallas de interpolación de alta resolución. Esto puede hacer que el KED sea menos práctico para aplicaciones en tiempo real o para conjuntos de datos muy grandes.
d. Necesidad de una malla de interpolación: El KED requiere la creación de una malla de interpolación con valores de la variable externa para cada punto de la malla. Esto puede ser un desafío si no se dispone de datos de la variable externa en toda la extensión de la malla.
e. Dificultad de interpretación: Aunque el KED puede proporcionar estimaciones más precisas que otros métodos de interpolación, la interpretación de los resultados puede ser más difícil. Esto se debe a la inclusión de la variable externa y a la complejidad del modelo de KED en sí.
A pesar de sus desventajas, el KED es valioso para la interpolación de datos espaciales. Su eficacia depende de su uso adecuado y del entendimiento de sus limitaciones.
Las 5 preguntas más comunes relacionadas con kriging con Deriva Externa:
¿Qué es la “deriva externa” en el KED? La “deriva externa” se refiere a la inclusión de una variable externa en el modelo de Kriging. Esta variable externa, que puede ser cualquier característica medible que se espera que esté correlacionada con la variable de interés, se utiliza para explicar parte de la variación espacial en los datos.
¿Cómo elijo la variable externa en el KED? La elección de la variable externa debe basarse en el conocimiento del sistema que estás estudiando. Idealmente, debería ser una variable que esté fuertemente correlacionada con la variable de interés y que esté disponible en todas las ubicaciones para las que quieres hacer estimaciones.
¿Por qué necesito verificar la normalidad de mis datos en el KED? Es esencial verificar la normalidad en el KED porque este método asume que los residuos (diferencias entre los valores observados y los estimados como tendencia) siguen una distribución normal. Si tus datos no cumplen esta suposición, las estimaciones podrían ser sesgadas o inexactas, por lo que puede ser necesario transformar tus datos para garantizar su normalidad antes de aplicar el KED.
¿Cómo manejo las tendencias en mis datos cuando uso KED? Las tendencias en los datos pueden ser manejadas en el KED a través de la función de deriva. Al incluir una función de deriva en tu modelo, puedes modelar la variación sistemática en tus datos que no puede ser explicada por la autocorrelación espacial.
¿Cuándo debería usar KED en lugar de Kriging ordinario? El KED puede ser útil cuando tienes una variable externa que está fuertemente correlacionada con tu variable de interés, o cuando tus datos muestran una tendencia espacial que no puede ser manejada adecuadamente por el Kriging ordinario.
#QGIS, #RStats, #Kriging, #SIG, #AnálisisEspacial, #VisualizaciónDeDatos, #Geoestadística, #CienciaDeDatos, #CódigoAbierto, #Teledetección.