Domina Kriging Universal: La Guía Definitiva Paso a Paso.
Si estás involucrado en proyectos ambientales, ya sabes lo importante que es obtener resultados precisos y confiables en la interpretación de datos espaciales. Para ayudarte a lograr esto, la comunidad GeoRGB ha creado la guía definitiva de Kriging Universal: una técnica efectiva para modelar y predecir datos espaciales.
En esta guía detallada, aprenderás a preparar tus datos de manera adecuada, incluyendo cómo eliminar la tendencia de los datos no deseada que pueden afectar la precisión de tus resultados. Además, descubrirás cómo seleccionar el modelo de Kriging Universal adecuado para tus proyectos de contaminación de suelos e hidrogeología.
La guía ha sido creada por expertos en datos espaciales de la comunidad GeoRGB y se encuentra disponible en línea en https://giscourse.online. Aquí, encontrarás todos los recursos que necesitas para dominar Kriging Universal, incluyendo videos tutoriales, ejemplos de casos de estudio y mucho más.
Aprender a aplicar Kriging Universal a tus proyectos de contaminación de suelos e hidrogeología puede ser la clave para lograr resultados precisos y confiables. ¡No te pierdas esta guía definitiva de Kriging Universal y descubre cómo puedes mejorar tus proyectos hoy mismo!
¿Qué es el kriging universal?
El kriging universal es un método de interpolación espacial que parte del supuesto de que el valor de una variable Z en un punto “s” se puede expresar como la suma de una función determinista μ(s) y un término estocástico ε(s).
Z(s)= μ(s)+ε(s)
La función determinista representa la tendencia espacial de los datos, que puede ser una función polinómica lineal u otra función determinista elegida a través del análisis exploratorio de datos. El error aleatorio representa la variabilidad local de los datos, que se modela mediante el variograma o la covarianza y se interpola mediante la técnica de kriging ordinario. El objetivo del kriging universal es estimar el valor de Z(s) en ubicaciones no muestreadas a partir de los valores observados y sus valores estocásticos associados.
En el caso del Kriging Universal, el cálculo de la tendencia espacial de los datos y el cálculo del Kriging Ordinario (a los valores residuales) se ejecutan de manera automática en un solo proceso. Sin embargo, si se tratan de manera independiente la tendencia y los valores residuales, estaríamos hablando de Kriging con Regresión.
Preparación de datos para Kriging Universal
Paso 1: Recopilación de datos
Para utilizar Kriging Universal, el primer paso es recopilar los datos espaciales necesarios, los cuales pueden ser obtenidos a través de mediciones directas en el campo, datos recopilados mediante sensores remotos, modelos digitales de elevación, entre otros. Es importante asegurarse de que los datos sean completos y precisos, ya que la calidad de los datos es crucial para obtener resultados validos con la interpolación a través de kriging universal.
Durante la captura de los datos, se recomienda registrar toda la información relevante, como la ubicación geográfica, la fecha y hora de la captura, la fuente de los datos y cualquier otra información que pueda ser relevante. Esto es especialmente importante en el caso de datos ambientales, como los datos de contaminación de suelos o agua.
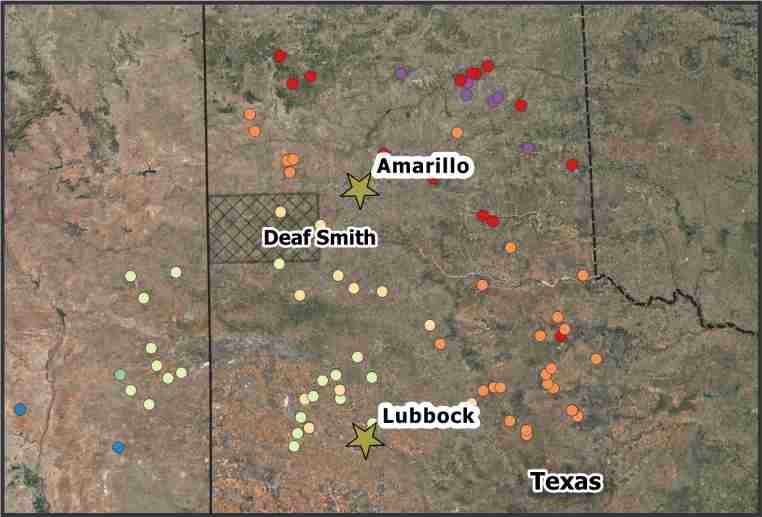
Distribucion espacial de los datos, graduados de acuerdo a la profundidad del agua subterranea.
Paso 2: Análisis exploratorio de datos
Para llevar a cabo un análisis exploratorio de datos, es posible utilizar herramientas de visualización, como por ejemplo, histogramas, gráficos de cajas, gráficos de dispersión, etc. Estas herramientas permiten examinar la distribución de los datos y detectar valores atípicos o errores que podrían afectar la precisión de los resultados.
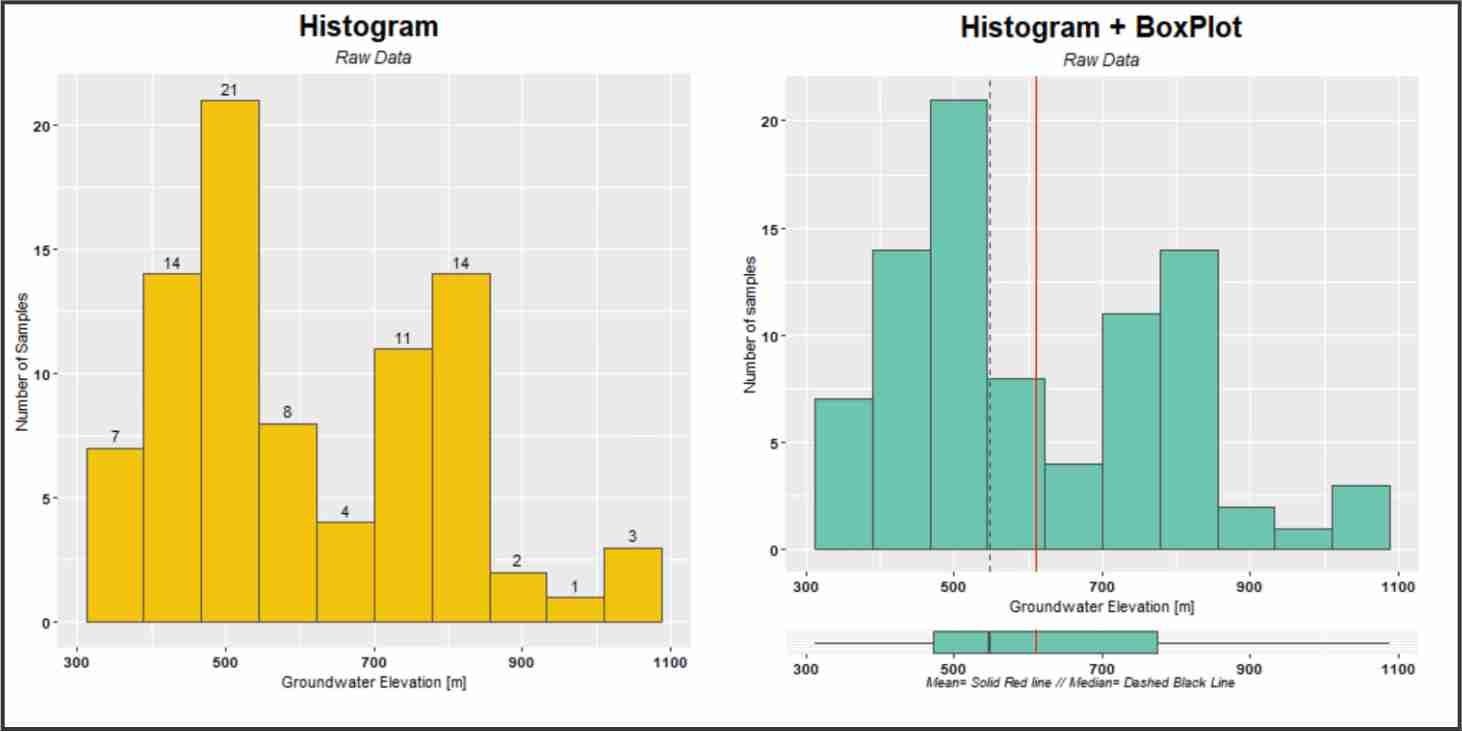
Izquierda: histograma con el numero de mustras encima de cada contenedor. Derecha: Histograma y diagrama de caja juntos, con la media y la mediana.
En particular, la presencia de tendencias en los datos puede ser un desafío importante para el análisis espacial. Las tendencias pueden deberse a factores como gradientes topográficos, variaciones en la intensidad de la fuente, el gradiente hidráulico, entre otros. Es importante identificar estas tendencias y determinar su naturaleza antes de continuar con el proceso de Kriging Universal. Cabe destacar que, en el Kriging Universal, la tendencia se define a través de las coordenadas, mientras que en el kriging con deriva externa la tendencia se define a través de cualquier otro tipo de variable.
En algunos casos, la tendencia puede ser trabajada directamente con kriging universal. En otros casos, es posible que sea necesario utilizar técnicas más avanzadas, como kriging con regresión, para modelar la tendencia y los valores residuales separadamente.
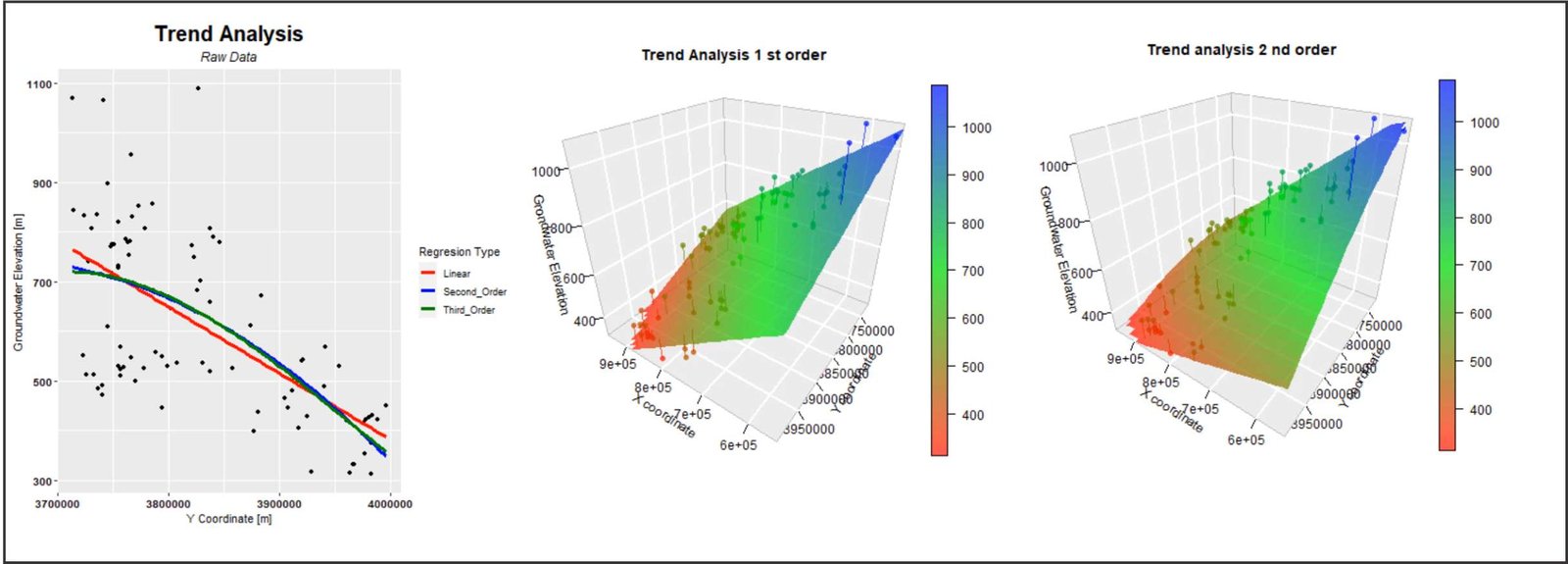
Izquierda: análisis de tendencia en relación a las coordenadas Y. Centro: modelo 3D donde se muestra el plano de la tendencia con un polinomio de primer order y los valores de las muestras. Derecha: modelo 3D donde se muestra el plano de la tendencia con un polinomio de segundo order y los valores de las muestras.
Paso 3: Transformación de datos
En algunos casos, puede ser necesario transformar los datos antes de realizar Kriging Universal. Por ejemplo, si los datos tienen una distribución no normal, se pueden transformar mediante una transformación logarítmica, una transformación de raíz cuadrada, o una transformación Box-Cox, entre otras. Sin embargo, cuando se trabaja con kriging universal, los datos que se van a interpolar son los residuales, no los datos originales. Por consiguiente, para garantizar resultados precisos, es necesario que los datos residuales tengan una distribución normal o cercana a ella. La transformación de los datos originales puede ayudar a mejorar la distribucion de los datos residuales y con ello, la precisión de los resultados del Kriging Universal.
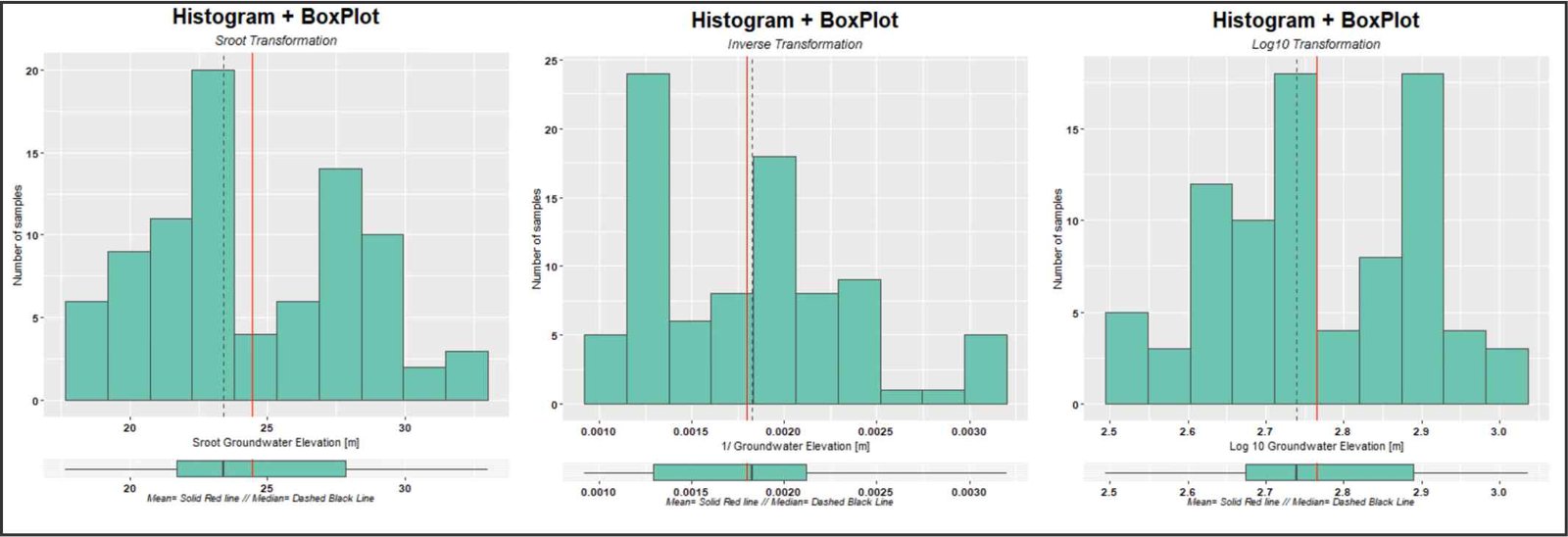
Transformación de los datos originales. Izquierda: transformación basada en la raíz cuadrada. Centro: transformación basada en el inverso. Derecha: transformación basada en el logaritmo de base 10.
Paso 4: Análisis exploratorio de datos sobre valores residuales
En primer lugar, es importante destacar que el análisis variográfico se debe realizar sobre los datos residuales, ya que éstos se utilizarán en el modelo estocástico dentro del proceso de Kriging Universal. Además, los datos residuales deben cumplir una serie de requisitos para poder ser utilizados para la interpolación con Kriging Ordinario. Concretamente, se requiere realizar un análisis de datos sobre los valores residuales para garantizar la viabilidad de los mismos.
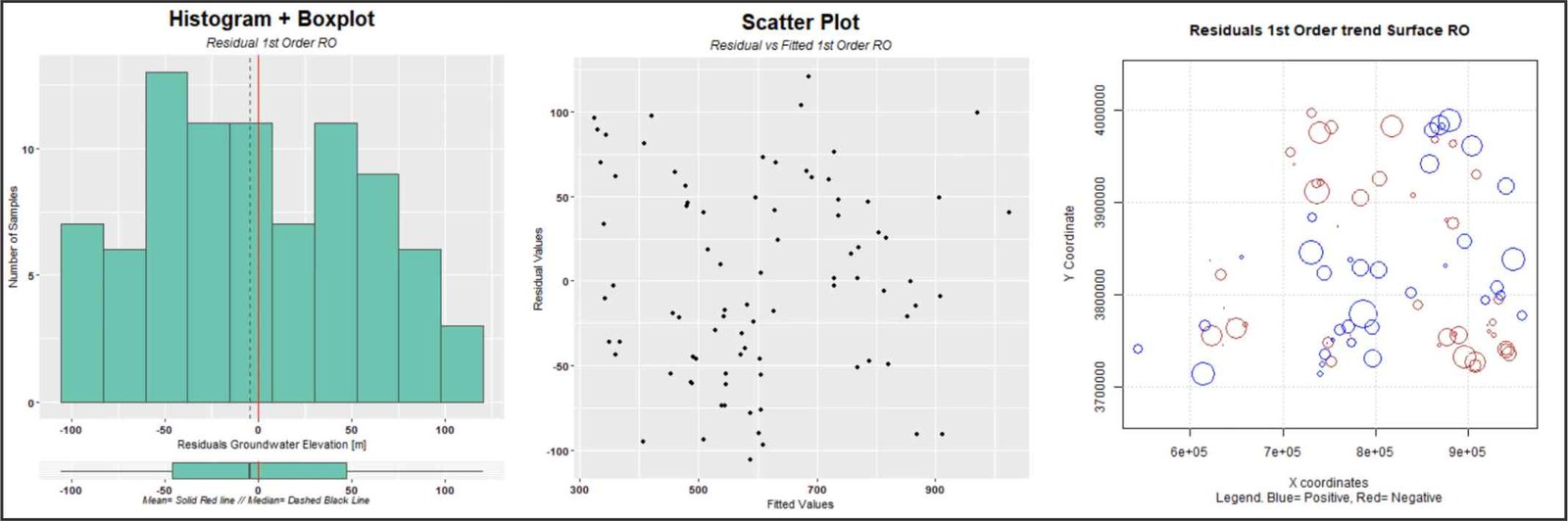
Análisis de los valores residuales. Izquierda: histograma y diagrama de caja. Centro: diagrama de dispersión de los valores predichos y residuales. Derecha: diagrama de burbujas.
Paso 5: Análisis variográfico
Una vez finalizado el análisis exploratorio de los valores residuales, se procede al análisis variográfico. El análisis variográfico implica la construcción de un modelo matemático que explique la relacion entre la variabilidad de los datos y la distancia entre ellos. La función que se utiliza para analizar esta relacion es el variograma. El variograma describe cómo la varianza de los datos cambia a medida que aumenta la distancia entre ellos.
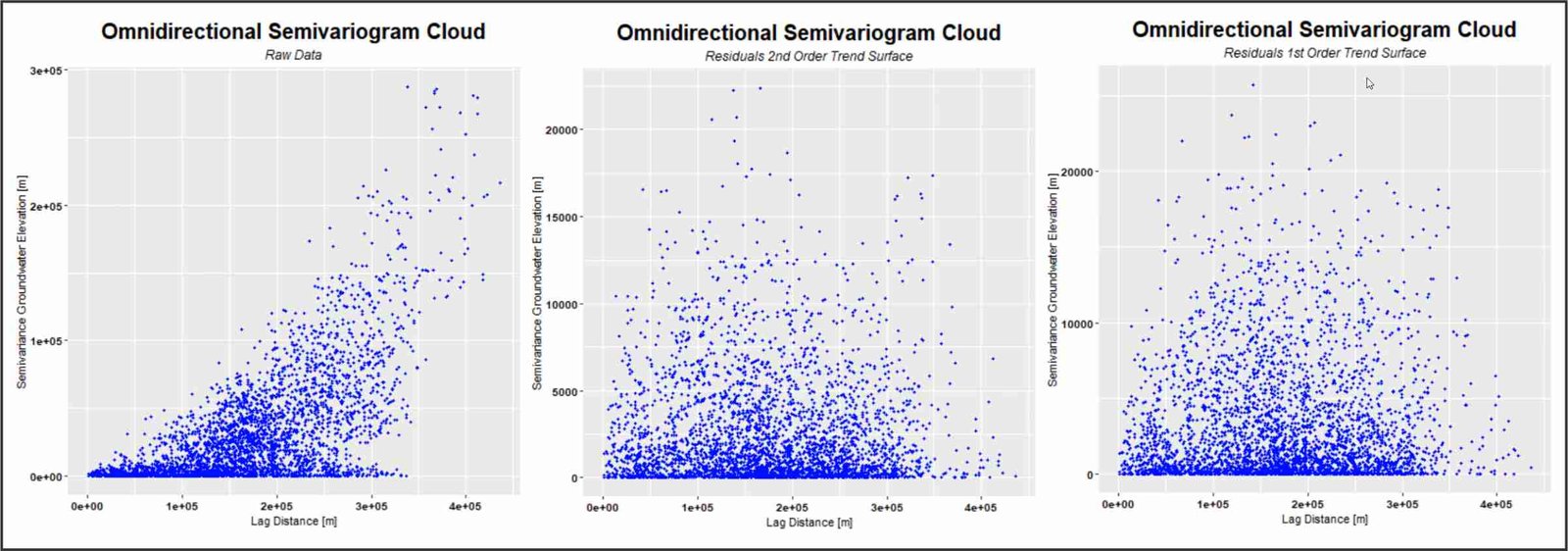
Análisis variográfico de la nube del variograma omnidireccional. Izquierda:datos originales, donde la tendencia en los datos es obvia. Centro: datos procedentes de los residuos asociados con la superficie de tendencia de primer orden. Derecha: datos procedentes de los residuos asociados con la superficie de tendencia de segundo orden.
El análisis variográfico es una herramienta importante para entender la estructura de los datos espaciales. A través de él, se pueden obtener diferentes parámetros como el rango, la autocorrelación espacial, el efecto nugget y la meseta parcial. Estos parámetros son relevantes para la modelización y predicción de valores espaciales, ya que permiten entender la variabilidad de los datos y cómo se relacionan espacialmente. El efecto nugget, por ejemplo, representa la variabilidad no explicada por la estructura espacial del variograma, mientras que la meseta parcial indica la cantidad de variabilidad que se puede explicar mediante la estructura espacial. Si la meseta parcial es alta, significa que hay una estructura espacial clara en los datos, lo que facilita la modelización del variograma y la realización del Kriging Universal.
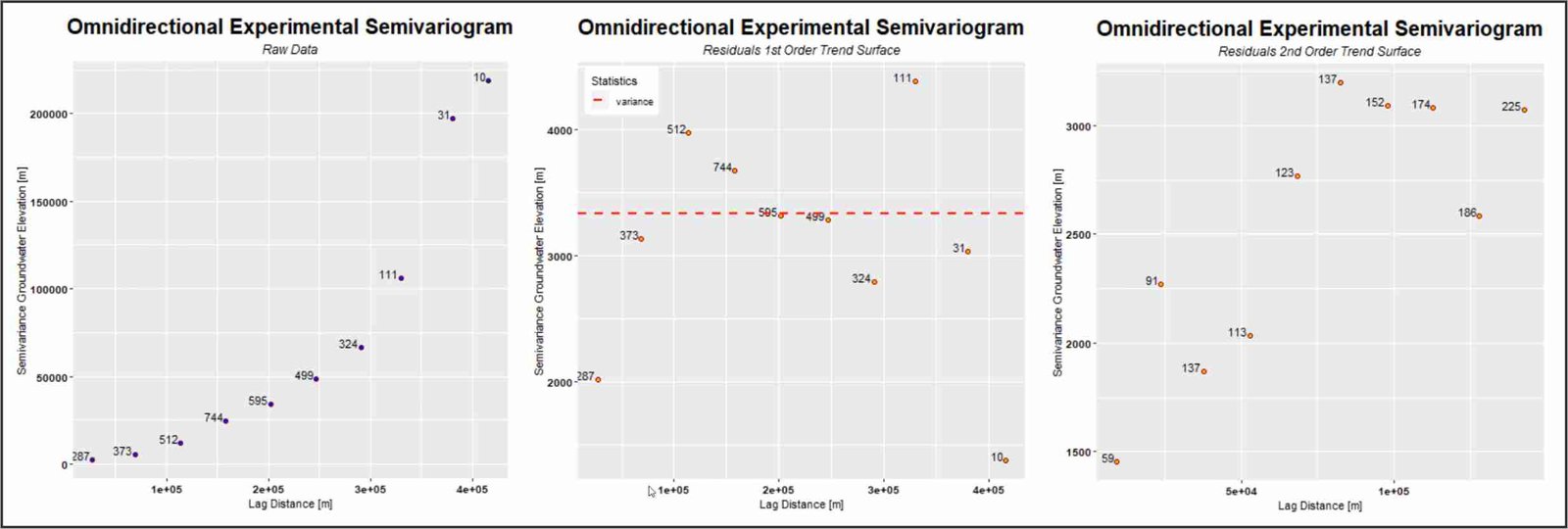
Análisis variográfico del variograma experimental omnidireccional. Izquierda:datos originales, donde la tendencia en los datos es obvia y de naturaleza cuadrática. Centro: datos procedentes de los residuos asociados con la superficie de tendencia de primer orden. Derecha: datos procedentes de los residuos asociados con la superficie de tendencia de segundo orden.
Paso 6: Selección del modelo del variograma
Una vez creado el variograma y se procede a seleccionar el modelo que mejor se ajuste a los datos. El modelo del variograma es una función matemática que describe la estructura de correlación espacial de los datos. Esta estructura queda perfectamente cuantificada con los valores del rango, la meseta parcial y el efecto nugget.
La selección del modelo del variograma adecuado es crucial para obtener resultados precisos en el Kriging Universal. Existen varios modelos de variograma disponibles, cada uno con sus propias ventajas y desventajas. Algunos de los modelos de variograma más comunes incluyen el modelo esférico, el modelo exponencial y el modelo gaussiano.
La selección del modelo del variograma no es una tarea fácil. Esta selección se basa en la distribución de los datos del variograma y en la elección de un modelo adecuado. Por lo tanto, se requiere un análisis cuidadoso para lograr una buena selección del modelo del variograma. Al final, es recomendable probar varios modelos de variograma para determinar el más adecuado a los datos disponibles.
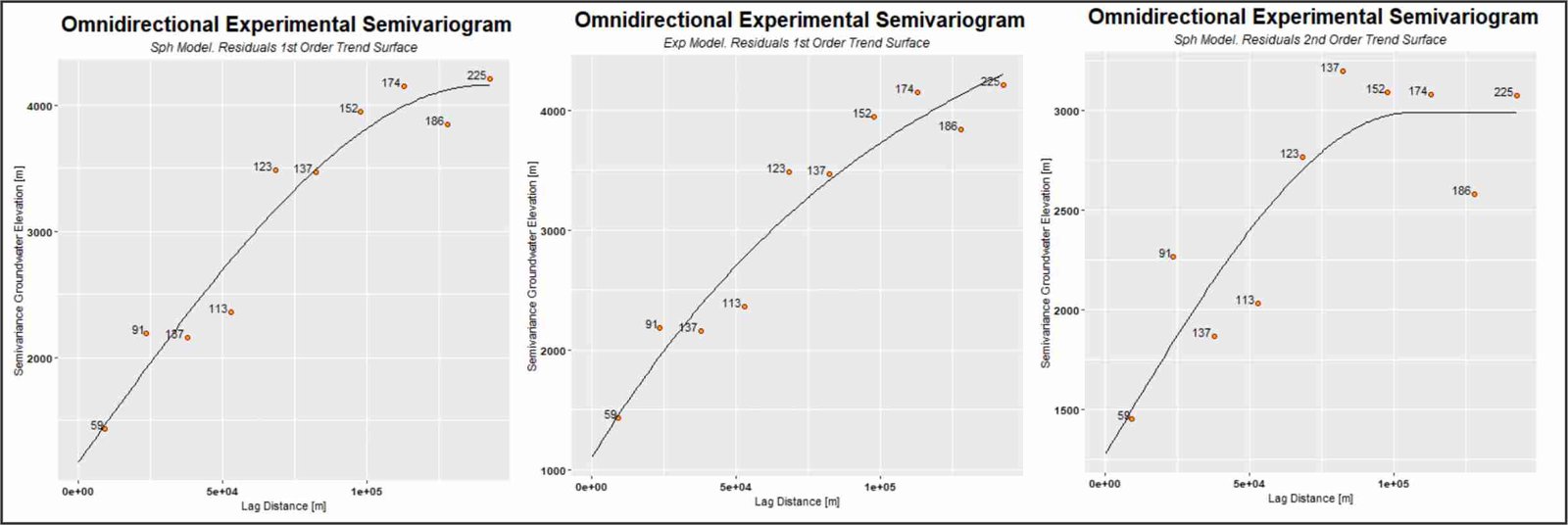
Izquierda: modelo esférico ajustado a los valores residuales procedentes del plano de tendencia de primer orden. Centro: modelo exponencial ajustado a los valores residuales procedentes del plano de tendencia de primer orden. Derecha: modelo esférico ajustado a los valores residuales procedentes del plano de tendencia de segundo orden.
Paso 7: Validación y verificación del modelo de semivariograma en Kriging Universal
Después de seleccionar el modelo de semivariograma, es importante validar y verificar el modelo. Una forma común de hacerlo es mediante la técnica de validación cruzada, donde se divide el conjunto de datos en grupos y se realiza el análisis en cada grupo para evaluar la precisión del modelo. También es importante utilizar otros mecanismos de evaluación, como la comparación de los valores observados y los valores predichos.
Además, se debe prestar atención al efecto del tamaño de la vecindad y la densidad de muestreo en el modelo de semivariograma. Una baja densidad de muestreo puede afectar la precisión del modelo, mientras que una vecindad demasiado grande puede hacer que el modelo sea demasiado generalizado y no pueda capturar la variabilidad local de los datos.
En resumen, es crucial realizar una validación y verificación rigurosas del modelo de semivariograma en Kriging Universal para asegurar la precisión y fiabilidad de los resultados.
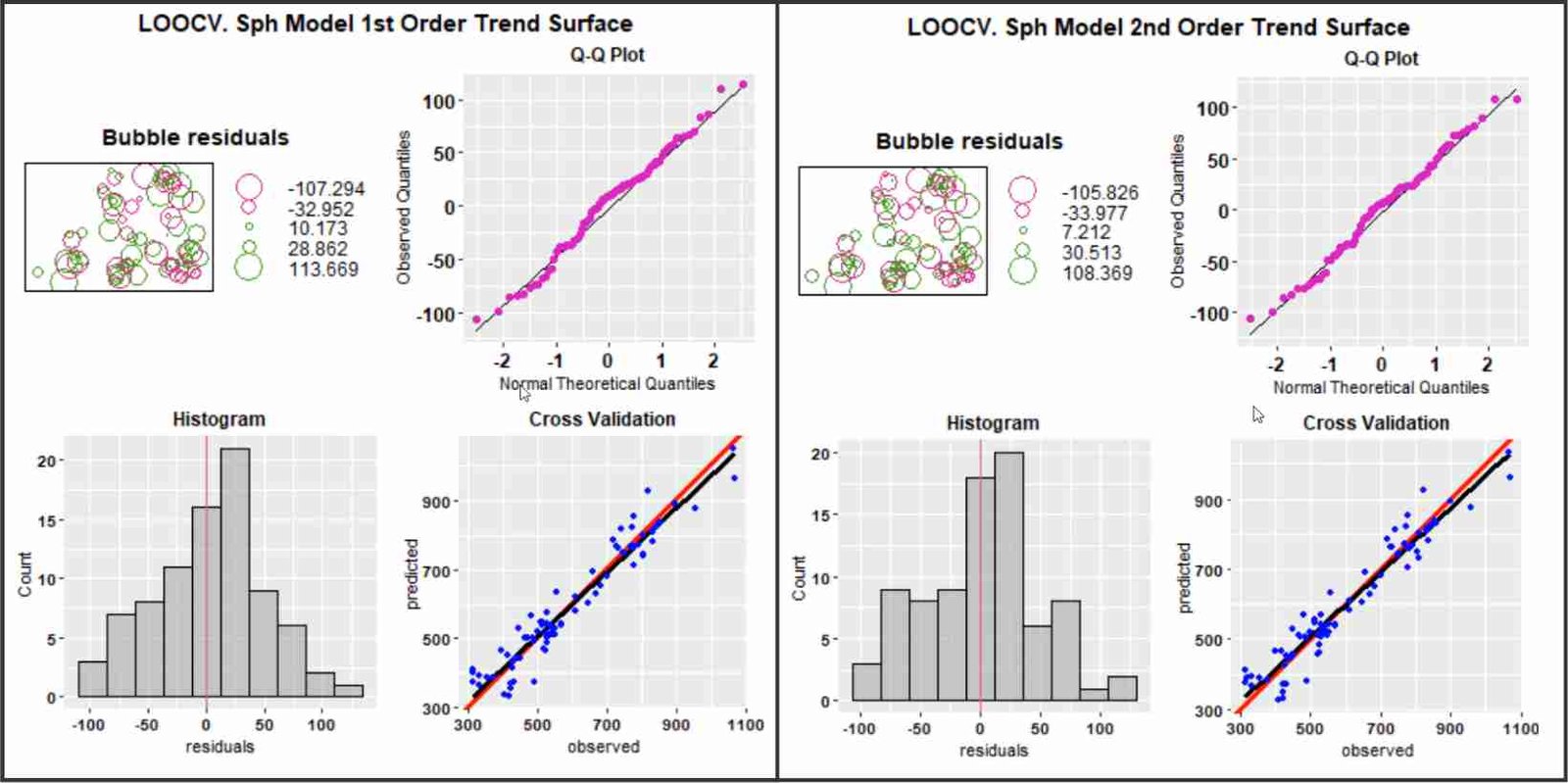
Validación cruzada dejando uno fuera (LOOCV) para el modelo esférico. Izquierda: modelo kriging basado en valores residuales procedentes de la superficie de tendencia de primer orden. Derecha: modelo kriging basado en valores residuales procedentes de la superficie de tendencia de segundo orden.
Paso 8: Interpolación usando Kriging Universal
Al final, el kriging universal es la suma del modelo estocástico (kriging ordinario) y del modelo determinista (superficie de tendencia). El kriging universal combina estos dos modelos de forma totalmente automática. Esta combinacion es posible a traves de la información proporcionada durante los pasos anteriores. Como por ejemplo, la selección de la superficie de tendencia y el modelo de semivariograma. La interpolación resultante se puede utilizar para generar mapas de contorno y superficies de distribución espacial de los datos. Esta informacion puede ser útil en la toma de decisiones en proyectos ambientales y otros campos relacionados.
Es importante tener en cuenta que la precisión de la interpolación depende de la calidad de los datos utilizados. Además, también depende de la elección adecuada del modelo de semivariograma. Por lo tanto, es crucial considerar ambos factores para obtener una interpolación precisa. Adicionalmente, es necesario realizar una validación cruzada y otros mecanismos de evaluación para garantizar la fiabilidad de los resultados.
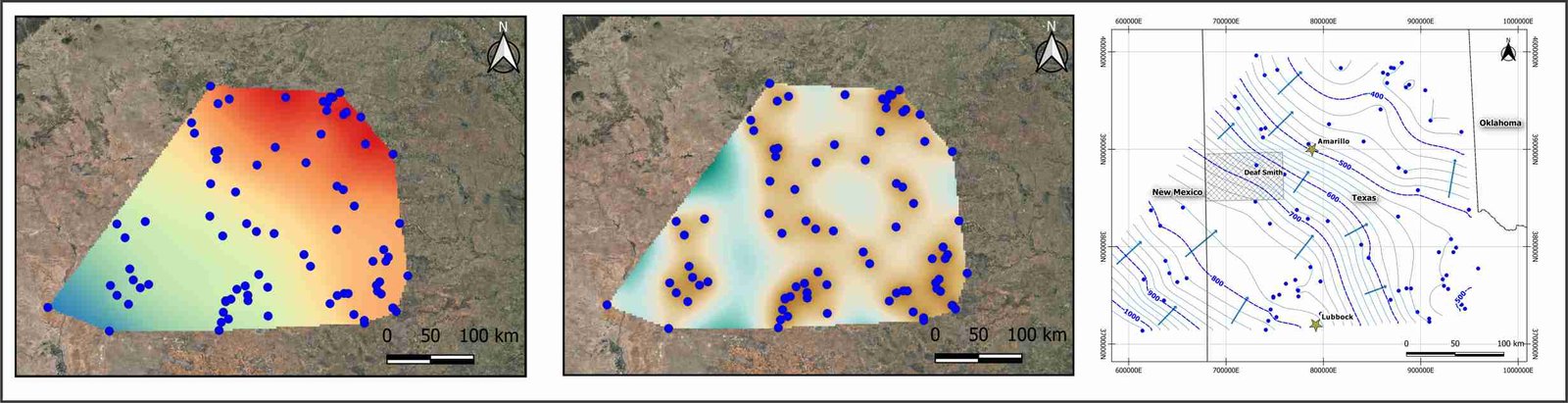
Resultado final de la interpolación. Izquierda: se muestra el mapa de la predicción. Centro: se muestra el mapa de errores, varianza. Derecha: mapa de contorno en función de los valores de la predicción.
Ejemplo práctico con QGIS y R, basado en kriging universal
A continuación, presentamos el primer tutorial de una serie de ocho videos que muestran un ejercicio práctico del kriging universal. El tutorial proporciona una descripción detallada de los ocho pasos principales involucrados en el proceso de interpolación. El proyecto se enfoca en evaluar la dirección del flujo de agua subterránea para establecer un sitio de residuos nucleares en los Estados Unidos.
Durante el tutorial, el instructor guía al espectador a través de las diversas etapas del proceso de interpolación. Es un tutorial paso a paso, desde la entrada y exploración de datos hasta la aplicación del kriging universal. Al final del ejercicio práctico se hará una interpretación de los resultados. El video está diseñado para ser fácil de seguir y accesible, lo que permite que cualquier persona con conocimientos básicos de GIS y R participe en el ejercicio.
Al finalizar la serie de ocho videos, los espectadores habrán adquirido experiencia práctica en el uso del kriging universal. Además, contarán con las habilidades necesarias para aplicar este método en sus propios proyectos. Los conocimientos obtenidos se pueden aplicar en campos como la geología y las ciencias ambientales, entre otros. El objetivo final es adquirir habilidades en el análisis de datos espaciales utilizando diversas herramientas.
Primera lección del cuarto curso de Geoestadística: Interpolación y mapeo de kriging/cokriging, impartido en https://giscourse.online/
Conviértete en un experto en geoestadística hoy mismo
Si estás buscando expandir tus habilidades en análisis geostadístico, ¡este curso es para ti!. Este Curso de Geostadística sobre Interpolación y Mapeo Kriging/Cokriging te brindará una comprensión profunda de los diferentes tipos de Kriging. Lo cual, te facilitara el análisis de datos espaciales y la creación de mapas totalmente profesionales. El curso presenta ejemplos reales y ejercicios prácticos utilizando R integrado en QGIS. No cabre duda, que es la elección perfecta para aquellos que deseen llevar su análisis geoestadístico al siguiente nivel. No esperes más, ¡accede ahora y comienza a aprender hoy!.

Ventajas del kriging universal
- Toma en cuenta la distribución espacial de los datos: el kriging universal utiliza la información sobre la distribución espacial de los datos para estimar los valores desconocidos en lugares donde no se dispone de datos.
- Produce estimaciones precisas y confiables: debido a su enfoque estadístico, el kriging universal produce estimaciones precisas y confiables de los valores desconocidos en el área de estudio.
- Considera la variabilidad espacial de los datos: el kriging universal utiliza la información sobre la variabilidad espacial de los datos para producir una estimación más precisa en los lugares donde los datos son más variables.
- Flexibilidad en la elección de la tendencia: el kriging universal permite la inclusión de una tendencia determinista en los datos, lo que lo hace más flexible en la elección de la forma de la tendencia.
- Capacidad para modelar la estructura de la variabilidad espacial: el kriging universal permite la modelación de la estructura de la variabilidad espacial de los datos, lo que permite una mayor precisión en la interpolación de los valores desconocidos.
- Permite la evaluación de la incertidumbre: el kriging universal proporciona una estimación de la incertidumbre asociada a la interpolación de los valores desconocidos.
Desventajas del kriging universal:
- Mayor complejidad: debido a que el kriging universal incorpora un modelo determinista de tendencia, el proceso de interpolación se vuelve más complejo en comparación con el kriging ordinario. Esto puede dificultar la implementación y el análisis de los resultados.
- Mayor requerimiento de datos: para ajustar adecuadamente el modelo de tendencia en el kriging universal, se necesitan más datos en comparación con el kriging ordinario. Esto puede ser una desventaja si los datos son costosos de obtener o están limitados en cantidad.
- Mayor sensibilidad a errores en la tendencia: si el modelo de tendencia utilizado en el kriging universal es incorrecto o está mal especificado, esto puede afectar significativamente la precisión de los resultados. Esto puede ser especialmente problemático si no hay una comprensión adecuada de la estructura de la tendencia en los datos.
- Mayor complejidad computacional: el kriging universal puede requerir más recursos computacionales debido a la necesidad de ajustar tanto la tendencia como la variabilidad de los datos. Esto puede hacer que el proceso sea más lento y menos eficiente en comparación con otros métodos de interpolación.
Las 5 preguntas más importantes relacionadas con kriging universal.
- ¿Qué es el kriging universal y cómo funciona?
Respuesta: Es un método de interpolación espacial que combina un modelo determinista (tendencia) con un modelo estocástico (kriging ordinario). El modelo estocástico se utiliza para modelar la variabilidad espacial de los datos. Por otro lado, el modelo determinista se utiliza para modelar cualquier tendencia espacial en los datos.
- ¿Cuáles son las ventajas del kriging universal sobre otros métodos de interpolación espacial?
Respuesta: Una de las principales ventajas del kriging universal es que puede manejar datos con tendencias espaciales y no estacionarias. También es una técnica robusta que se basa en modelos matemáticos sólidos y que puede proporcionar resultados precisos y confiables.
- ¿Cómo puedo validar los resultados de la interpolación de kriging universal?
Respuesta: La validación cruzada es una técnica comúnmente utilizada para evaluar la precisión de la interpolación de kriging universal. También se pueden utilizar otros métodos de validación, como la comparación con datos de validación independientes.
- ¿Cuáles son las ventajas del kriging universal en comparación con otros métodos de interpolación?
Respuesta: El kriging universal considera la variabilidad y la tendencia en datos espaciales para mayor precisión en la interpolación. Se utiliza para predecir valores en cualquier ubicación dentro del área de estudio, incluso donde no se hayan tomado muestras.
- ¿Cómo se selecciona el modelo de tendencia en el kriging universal?
En el kriging universal, el modelo de tendencia se selecciona a través del análisis exploratorio de datos. Además, este modelo puede ser únicamente lineal, lo que representa una de las mayores limitaciones del kriging universal. Si se desea un modelo no lineal, se necesita utilizar el kriging con regresión. El objetivo es encontrar un modelo que capte la tendencia espacial de los datos sin sobre ajustarse.
Las 5 preguntas más comunes relacionadas con kriging universal.
- ¿Qué es el kriging universal y cómo difiere del kriging ordinario?
Respuesta: El kriging universal combina un modelo determinista de tendencia con un modelo estocástico. A diferencia del kriging ordinario, que únicamente es un modelo estocástico. En definitiva, el kriging universal permite la incorporación de una tendencia espacial en los datos.
- ¿Cómo se selecciona el modelo de semivariograma en el kriging universal?
Respuesta: La selección del modelo de semivariograma en el kriging universal se basa en el análisis variográfico de los datos. Los modelos de semivariograma se ajustan a los datos para encontrar el mejor ajuste de la variabilidad.
- ¿Qué son los valores residuales en el kriging universal?
Respuesta: Los valores residuales son la diferencia entre los valores observados y los valores predichos por el modelo de tendencia. Estos valores residuales se utilizan para la interpolación espacial mediante el modelo estocástico de la función de semivariograma.
- ¿Cuáles son las ventajas del kriging universal?
Respuesta: El kriging universal permite incorporar una tendencia espacial y proporcionar estimaciones precisas de valores desconocidos. Adicionalmente, tiene la capacidad de proporcionar estimaciones de incertidumbre, lo que es una ventaja importante en la toma de decisiones.
- ¿Cuáles son las limitaciones del kriging universal?
Respuesta: El kriging universal tiene limitaciones en la elección del modelo de semivariograma. Esto se debe a la necesidad de tener datos suficientes y representativos para estimar la tendencia y variabilidad. Además, es necesario que los datos cumplan con suposiciones de estacionariedad y normalidad para la resolucion del modelo estocástico.
#QGIS, #RStats, #Kriging, #SIG, #AnálisisEspacial, #VisualizaciónDeDatos, #Geoestadística, #CienciaDeDatos, #CódigoAbierto, #Teledetección.