Kriging Ordinario en 5 Pasos: Una Guía Definitiva.
¡Bienvenido al fascinante mundo del kriging ordinario! ¿Sabías que esta técnica de interpolación espacial es utilizada en diversas disciplinas, desde la predicción del tiempo hasta la evaluación de la calidad del aire y la distribución de la contaminación? Si estás interesado en aprender más sobre cómo aplicar esta herramienta en tus análisis espaciales, estás en el lugar correcto. En esta guía definitiva, creada por la Comunidad GeoRGB y disponible en https://giscourse.online, te presentamos los 5 pasos clave para realizar el kriging ordinario exitosamente. ¡Sigue cuidadosamente estos pasos y estarás en el camino para obtener resultados precisos y confiables en tus proyectos científicos! Descubre cómo esta técnica te ayudará a comprender mejor los datos espaciales y a tomar decisiones informadas en tus investigaciones. ¡Acompáñanos en este viaje y aprendamos juntos!
Paso 1: Recopilar datos para trabajar con kriging ordinario
La recopilación de datos es un paso crítico en el proceso de kriging ordinario, ya que la precisión y la confiabilidad de los resultados de la interpolación dependen de la calidad y representatividad de los datos. En este sentido, es fundamental definir claramente la finalidad de la recopilación de datos y el área de estudio, lo que permitirá identificar qué tipos de datos son necesarios y cuáles son las fuentes de datos disponibles.
Para la recopilación de datos, se pueden utilizar diferentes fuentes, como estaciones meteorológicas, sensores remotos y mediciones de campo. Estos datos pueden incluir mediciones de calidad del aire, precipitación, temperatura, contaminación y otros parámetros ambientales. Es importante asegurarse de que los datos sean representativos del área de estudio y que cubran un período de tiempo suficiente para poder capturar las variaciones temporales y espaciales de los parámetros ambientales.
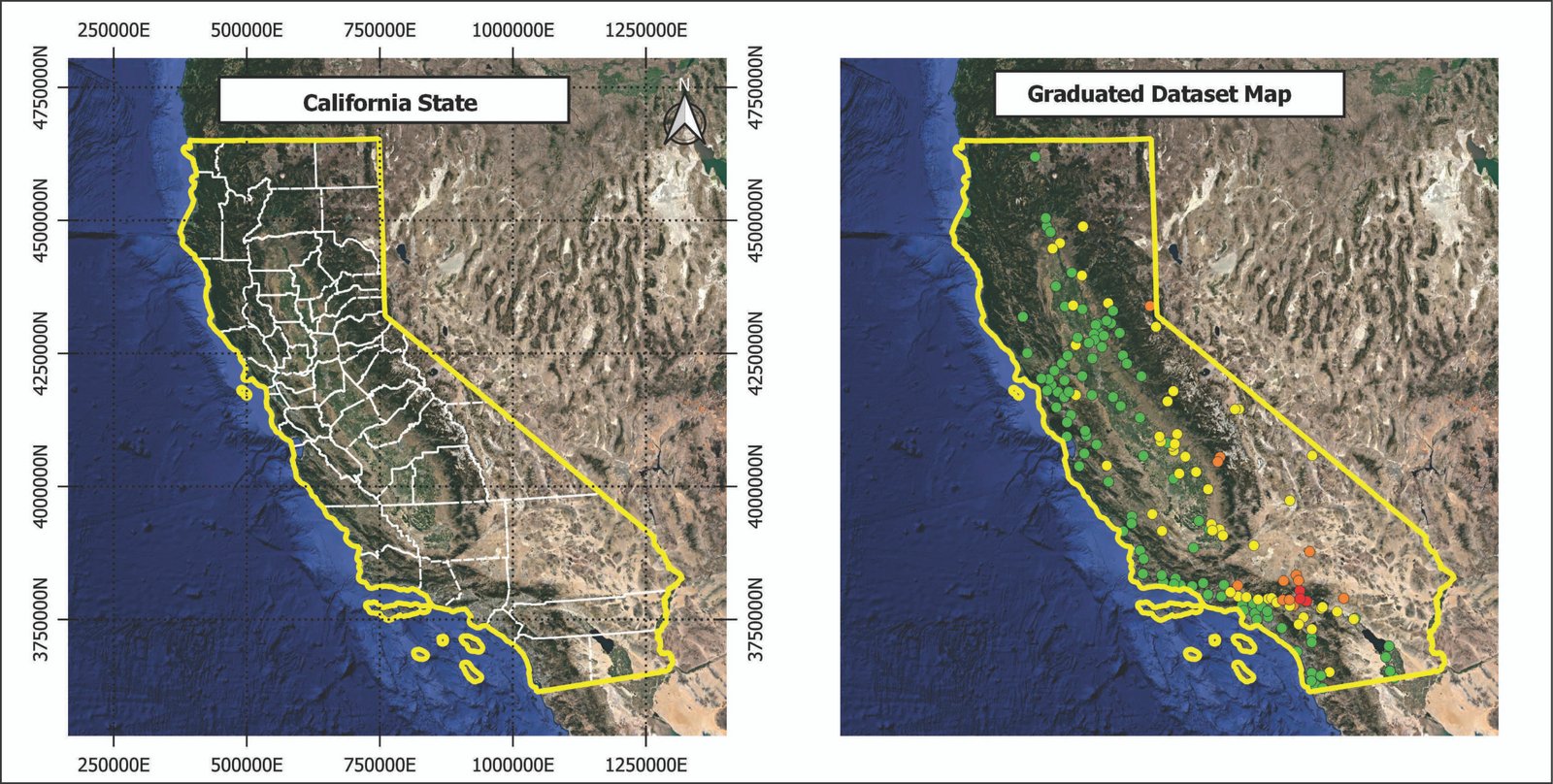
Izquierda: mapa que muestra el estado de California. Derecha: mapa que muestra la distribución espacial de los datos.
Una vez que se han recopilado los datos, es importante realizar un control de calidad para asegurarse de que sean precisos y confiables. Para ello, se pueden utilizar diferentes técnicas, como el cálculo de estadísticas de resumen y la detección de valores atípicos y errores. También es importante documentar adecuadamente los datos y la metodología de recopilación. Con ello, se podrá garantizar la transparencia y la reproducibilidad de los resultados.
Paso 2: Análisis exploratorio de datos para kriging ordinario
En este paso se lleva a cabo un análisis estadístico básico de los datos, con el objetivo de identificar la existencia de valores extremos, la distribución de las variables y la existencia de correlaciones.
En el análisis exploratorio de datos, se pueden utilizar diferentes técnicas, como la visualización y la estadística descriptiva. La visualización es una herramienta útil para comprender la distribución espacial y temporal de los datos, y se pueden utilizar mapas y gráficos para identificar patrones y tendencias. Por otro lado, la estadística descriptiva se utiliza para resumir y analizar los datos, lo que puede incluir el cálculo de medidas de centralidad y dispersión, así como la identificación de posibles valores atípicos.
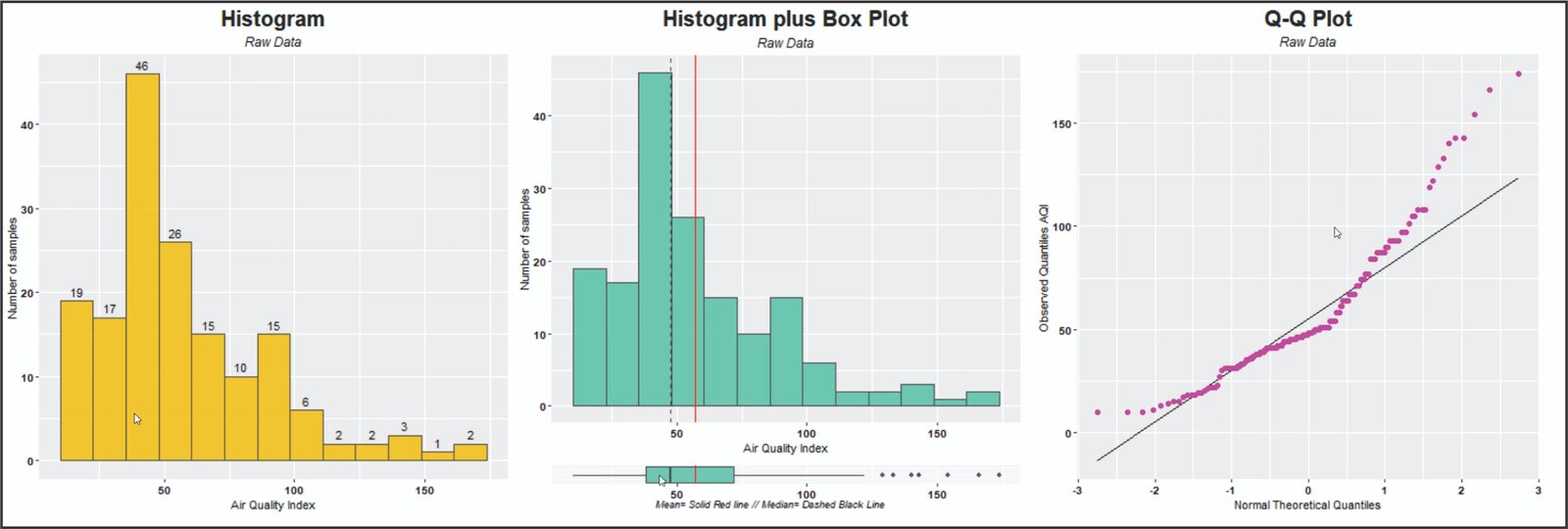
Izquierda: histograma con distribución asimétrica. Centro: mismo histograma, pero agregando el diagrama de caja. Derecha: gráfico Q-Q que indica la falta de normalidad de los datos.
Además, en el análisis exploratorio de datos, se debe considerar la estacionariedad del proceso. La estacionariedad implica que la distribución de los datos es constante en el tiempo y el espacio, lo que es importante para el uso del kriging. Si el proceso no es estacionario, se pueden utilizar técnicas de transformación para obtener una distribución estacionaria.
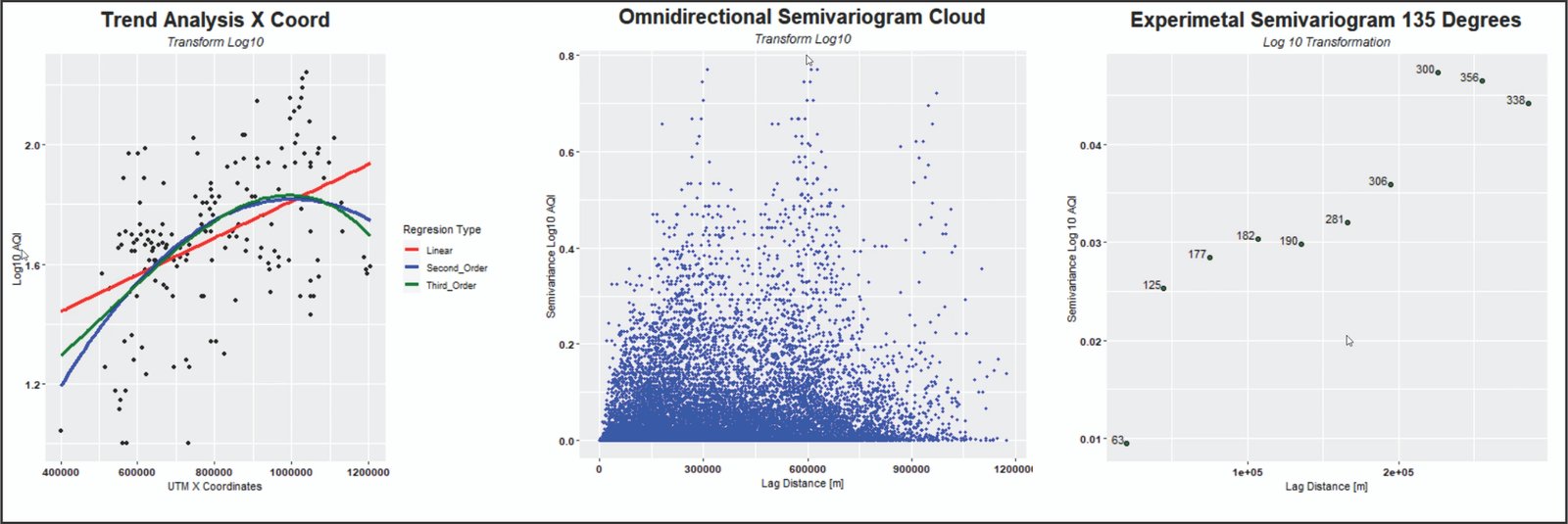
Izquierda: análisis de tendencia en relación a las coordenadas X. Centro: nube del semivariograma omnidireccional. Derecha: semivariograma experimental con una dirección de 135 grados.
Paso 3: Selección de modelo en kriging ordinario
En particular, en el proceso de selección de modelo para el kriging ordinario, la elección del modelo de variograma es crucial. Los modelos de variograma más utilizados son el esférico, el exponencial y el gaussiano. El modelo esférico es apropiado para datos con una correlación espacial corta. Por otro lado, el modelo exponencial es utilizado para datos con una correlación espacial moderada. Finalmente, el modelo gaussiano se utiliza para datos con una correlación espacial larga.
Es importante tener en cuenta que la elección del modelo de variograma puede afectar significativamente los resultados de la interpolación, por lo que se debe seleccionar cuidadosamente el modelo que mejor se adapte a los datos y la finalidad de la aplicación. Además, es importante ajustar los parámetros del modelo de variograma de manera apropiada, lo que puede implicar realizar diferentes ajustes y evaluaciones del modelo.
En general, la selección del modelo de variograma es una parte crucial del proceso de kriging ordinario. El modelo de variograma adecuado dependerá de la naturaleza y la distribución espacial de los datos. Además, es importante considerar la finalidad de la aplicación y la escala temporal y espacial del problema. Se debe seleccionar cuidadosamente el modelo de variograma. También , es muy importante ajustar los parámetros del modelo de manera adecuada para lograr una interpolación precisa y confiable.
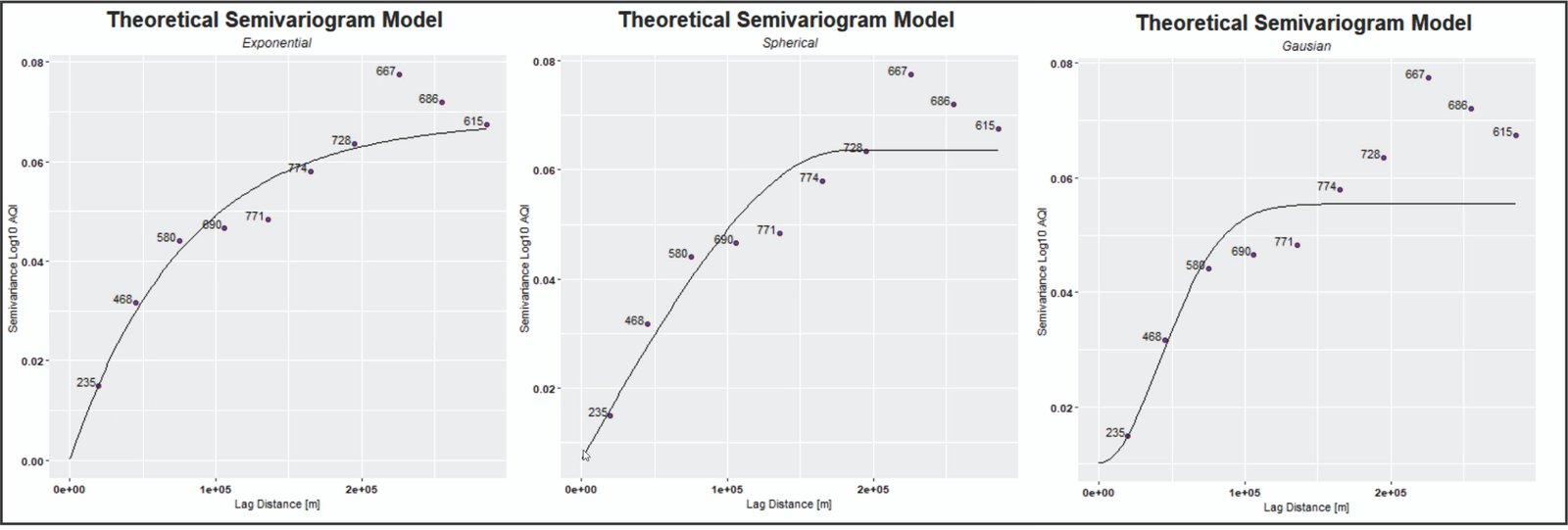
Izquierda: modelo Exponencial. Centro: modelo Esférico. Derecha: modelo Gaussiano.
Paso 4: Interpolación mediante kriging ordinario
El siguiente paso es realizar la interpolación utilizando el modelo de Kriging seleccionado. Esto implica la creación de una superficie continua a partir de los datos de muestra. Es importante tener en cuenta que los resultados de la interpolación dependen de la densidad de muestreo de los datos. Cuanto mayor sea la densidad de muestreo, más precisos serán los resultados de la interpolación.
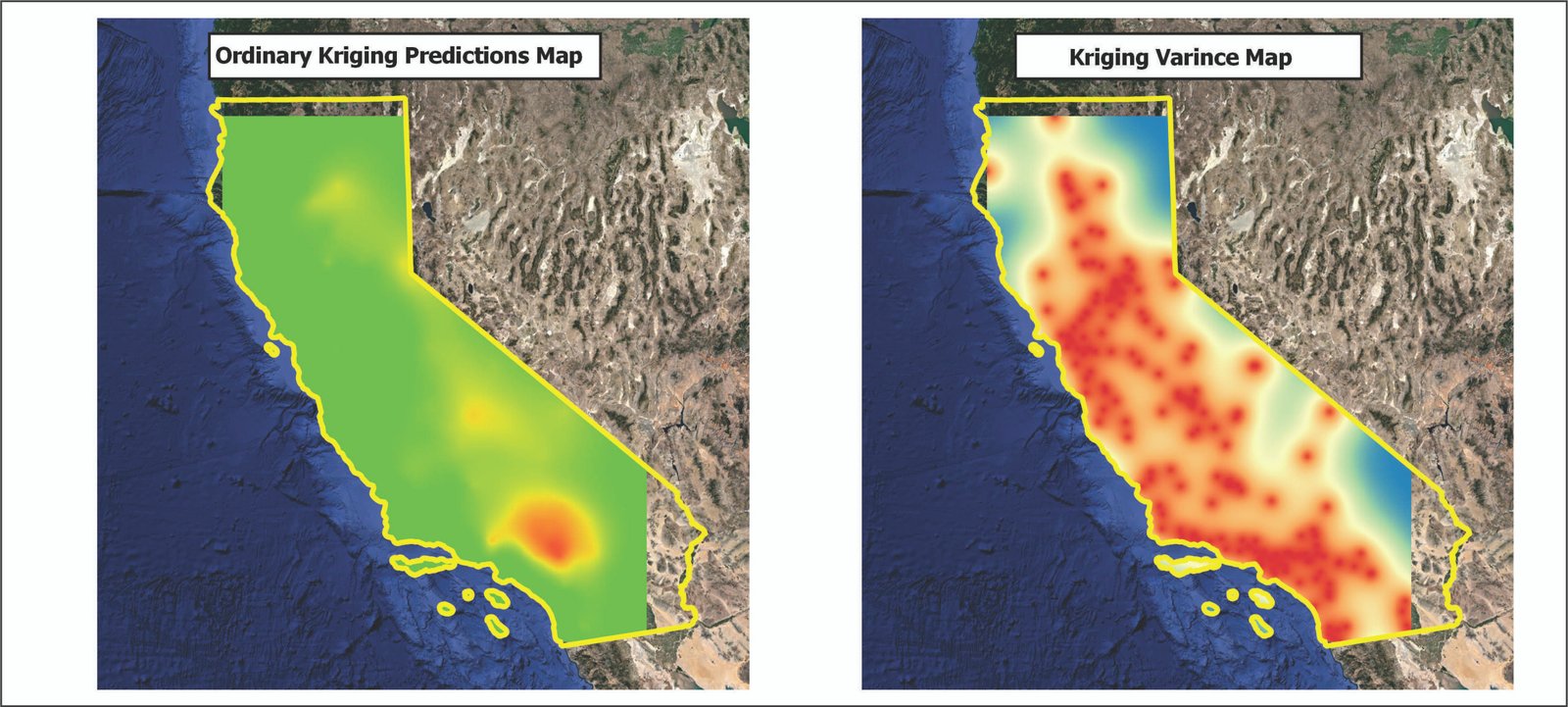
Izquierda: mapa que muestra la predicción de acuerdo al modelo kriging. Derecha: mapa que muestra la varianza de acuerdo al modelo kriging.
En este paso, se procede a aplicar el modelo de Kriging para interpolar los valores de la variable de interés en los puntos donde no se dispone de información. Es importante tener en cuenta que la precisión de los resultados dependerá del tamaño y distribución de los datos de muestra, así como del modelo de variograma seleccionado. También es importante tener en cuenta que la interpolación no proporcionará información precisa en áreas que están más allá del alcance de los datos de muestra. Por lo tanto, se debe tener precaución al interpretar los valores interpolados en áreas donde no hay datos de muestra.
Paso 5: Validación y Verificación del modelo de kriging ordinario
En la validación, se pueden utilizar diferentes técnicas. Una de las más populares es la validación cruzada, que se utiliza para evaluar la precisión del modelo de interpolación. La validación cruzada implica la partición de los datos de muestra en un conjunto de entrenamiento y un conjunto de validación. El conjunto de entrenamiento se utiliza para crear el modelo de Kriging, y el conjunto de validación se utiliza para evaluar la precisión del modelo. La validación cruzada puede proporcionar información sobre la capacidad del modelo para predecir valores desconocidos y la precisión de las predicciones en diferentes áreas del campo espacial.
La verificación, por otro lado, se utiliza para evaluar la calidad de los resultados de la interpolación. Esto puede implicar la comparación de los resultados de la interpolación con los datos de muestra y con otros datos de referencia, como mediciones independientes o estimaciones de otras técnicas de interpolación. La verificación es una forma importante de asegurarse de que los resultados de la interpolación sean precisos y confiables, y de detectar posibles errores o sesgos en el modelo de Kriging.
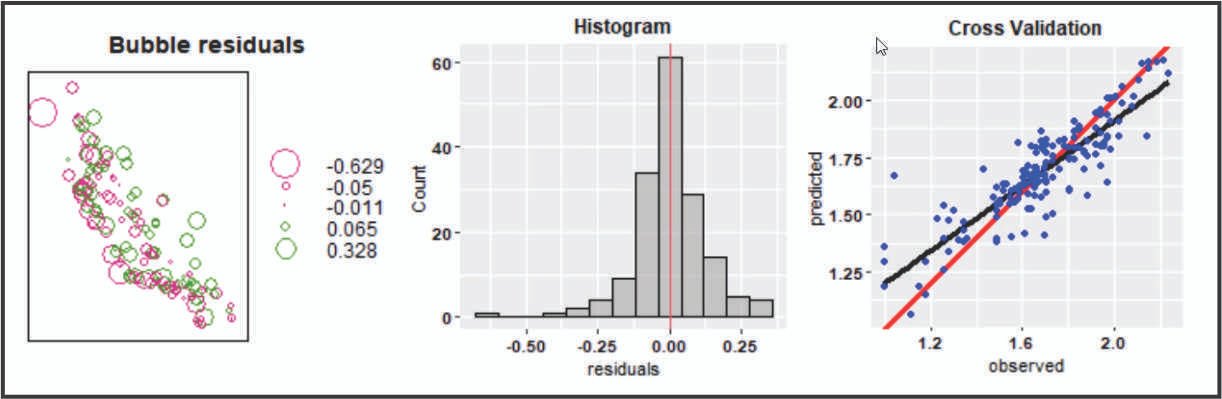
Validación cruzada dejando uno fuera (LOOCV) para el modelo esférico. Izquierda: mapa de burbujas para los valores residuales. Centro: histograma de los residuales. Derecha: gráfico de dispersión que muestra la relación entre los valores observados y los predichos.
En resumen, la validación y la verificación son pasos críticos en el proceso de kriging ordinario. Estos pasos permiten evaluar la precisión y la confiabilidad de los resultados de la interpolación, y detectar posibles errores o sesgos en el modelo. Es importante utilizar técnicas adecuadas de validación y verificación. Con estas técnicas, podemos garantizar la precisión y la confiabilidad de los resultados de la interpolación. Adicionalmente, podremos tomar decisiones informadas basadas en los datos interpolados.
Ejemplo práctico con QGIS y R basado en kriging ordinario
A continuación, te presentamos el primer tutorial, de una serie de 8 videos, en donde se realiza un ejercicio práctico. El tutorial incluye una descripción detallada de los cinco pasos principales para la realización de una interpolación mediante kriging ordinario. Este proyecto se enfoca en la evaluación de la contaminación atmosférica en el estado de California, en los Estados Unidos.
Primera lección del cuarto curso de Geoestadística: Interpolación y mapeo de kriging/cokriging, impartido en https://giscourse.online/
Conviértete en un experto en geoestadística hoy mismo
Si estás buscando expandir tus habilidades en análisis geostadístico, ¡este curso es para ti! El Cuarto Curso de Geostadística sobre Interpolación y Mapeo Kriging/Cokriging te brindará una comprensión profunda de los diferentes tipos de Kriging, así como la habilidad de aplicarlos a datos espaciales y presentar los resultados en mapas de una manera totalmente profesional. Con ejemplos reales y ejercicios prácticos utilizando R integrado en QGIS, este curso es la elección perfecta para aquellos que deseen llevar su análisis geoestadístico al siguiente nivel. No esperes más, ¡accede ahora y comienza a aprender hoy!

Ventajas del kriging ordinario
- Precisión: El kriging ordinario proporciona resultados precisos al estimar valores desconocidos en lugares donde no se dispone de datos medidos.
- Flexibilidad: El kriging ordinario se puede aplicar en una variedad de contextos y con diferentes tipos de datos.
- Interpretabilidad: El kriging ordinario proporciona un modelo matemático fácil de interpretar y utilizar. Este hecho, facilita enormemente el entendimiento de las relaciones espaciales entre los datos.
- Eficiencia: El kriging ordinario es computacionalmente eficiente y permite manejar grandes conjuntos de datos de forma rápida y eficaz.
- Actualización: El modelo de kriging ordinario se puede actualizar fácilmente con nuevos datos para mejorar los resultados de la interpolación. Con ello, se consigue una estimación más precisa en áreas donde se han recopilado nuevos datos.
Desventajas del kriging ordinario:
- Dependencia de la calidad de los datos: La precisión del kriging ordinario depende de la calidad de los datos de entrada. En consecuencia, contextos con baja calidad de los datos pueden representar un auténtico desafío.
- Sensibilidad a la elección de los parámetros: La elección de los parámetros del modelo en el kriging ordinario puede afectar significativamente la precisión de los resultados, lo que puede ser difícil de determinar en contextos con variabilidad espacial desconocida.
- Incapacidad para manejar datos no estacionarios: En el kriging ordinario, la elección de los parámetros puede afectar significativamente la precisión de los resultados. Por lo tanto, es difícil determinarlos en contextos con variabilidad espacial desconocida.
- No adecuado para grandes áreas de estudio: El kriging ordinario puede ser computacionalmente intensivo y no siempre es adecuado para grandes áreas de estudio, lo que puede limitar su aplicabilidad en algunos contextos.
- No proporciona incertidumbre espacial completa: El kriging ordinario proporciona estimaciones puntuales de valores desconocidos en lugares donde no se dispone de datos medidos, pero no proporciona una incertidumbre espacial completa, lo que puede ser una limitación en contextos donde la incertidumbre espacial es importante.
Las 5 preguntas más importantes relacionadas con kriging ordinario.
1. ¿Cómo se puede aplicar el kriging ordinario a diferentes tipos de datos?
La técnica kriging ordinario puede aplicarse a distintos tipos de datos, como datos puntuales, de área y de volumen. Esta técnica estima valores desconocidos en una malla de puntos mediante una función de correlación espacial.
2. ¿Cómo se pueden seleccionar los parámetros del modelo para maximizar la precisión de los resultados del kriging ordinario?
Los parámetros, como el modelo de variograma y el tamaño del vecindario, pueden seleccionarse ajustando la función de variograma y validando el modelo mediante técnicas como la validación cruzada.
3. ¿Cuáles son las limitaciones del kriging ordinario en términos de la variabilidad espacial y la calidad de los datos de entrada?
El kriging ordinario se ve afectado por la variabilidad espacial y la calidad de los datos de entrada, como la presencia de valores atípicos y la falta de muestras en áreas específicas.
4. ¿Cómo se puede incorporar la incertidumbre en los resultados del kriging ordinario?
La incertidumbre puede incorporarse en los resultados mediante la generación de mapas de incertidumbre basados en la función de variograma y la validación cruzada del modelo. Adicionalmente, la incertidumbre puede cuantificarse mediante la estimación del error estándar.
5. ¿Cuáles son las alternativas al kriging ordinario y cómo se comparan en términos de precisión y eficiencia en diferentes contextos?
Las alternativas incluyen la inversión de la distancia ponderada, el spline, la triangulación de Delaunay y los métodos basados en redes neuronales, y la elección dependerá del contexto y las propiedades de los datos.
Las 5 preguntas más comunes relacionadas con kriging ordinario.
1. ¿Qué es la función de variograma y cómo se utiliza en el kriging ordinario?
La función de variograma es una función matemática que describe la variabilidad espacial de los datos. En el kriging ordinario, se utiliza para modelar la correlación espacial y ajustar los parámetros del modelo.
2. ¿Cuál es el impacto de la calidad de los datos de entrada en la precisión del kriging ordinario?
La calidad de los datos de entrada puede afectar significativamente la precisión del kriging ordinario. La presencia de valores atípicos y la falta de muestras en áreas específicas pueden afectar la precisión de los resultados. Es por ello, que algunos casos requieren la aplicación de técnicas de preprocesamiento de datos y selección de muestras representativas.
3. ¿Cómo se puede implementar el kriging ordinario en un software de GIS?
Muchos software de GIS, como ArcGIS y QGIS, tienen herramientas que permiten implementar el kriging ordinario. El usuario puede ingresar los datos de entrada, seleccionar los parámetros del modelo y generar mapas de resultados y de incertidumbre.
4. ¿Cómo se puede manejar la anisotropía espacial en el kriging ordinario?
La anisotropía espacial varía en diferentes direcciones, y para manejarla se puede aplicar el kriging con anisotropía. Esta técnica modela la correlación espacial en diferentes direcciones y ajusta los parámetros del modelo en consecuencia.
5. ¿Cómo se puede abordar la falta de normalidad en los datos en el kriging ordinario?
La falta de normalidad en los datos pueden afectar la precisión del kriging ordinario. Sin embargo, se pueden utilizar técnicas de transformación de datos para abordar la falta de normalidad. Cabe mencionar, que existen diferentes técnicas para transformar los datos, como la logarítmica y la raíz cuadrada entre otras.
#QGIS, #RStats, #Kriging, #SIG, #AnálisisEspacial, #VisualizaciónDeDatos, #Geoestadística, #CienciaDeDatos, #CódigoAbierto, #Teledetección.